6 bài tập Một số bài toán tối ưu đơn giản (có lời giải)
55 người thi tuần này 4.6 581 lượt thi 6 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
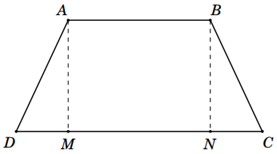
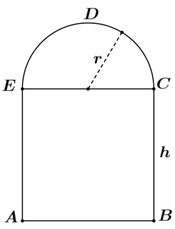
Gọi \(M,\,N\) lần lượt là hình chiếu vuông góc của \(A,\,B\) lên \(CD\)
Đặt \(x = MD\), \(\left( {0 < x < a} \right)\) suy ra \(AM = \sqrt {A{D^2} - M{D^2}} = \sqrt {{a^2} - {x^2}} \)
Diện tích của mảnh vườn hình thang cân là \(S\left( x \right) = \frac{{\left( {AB + CD} \right)AM}}{2} = \left( {a + x} \right)\sqrt {{a^2} - {x^2}} \).
Xét hàm số \(f\left( x \right) = \left( {a + x} \right)\sqrt {{a^2} - {x^2}} \)trên khoảng \(\left( {0 < x < a} \right)\)
Đạo hàm \(f'\left( x \right) = \frac{{ - 2{x^2} - ax + {a^2}}}{{\sqrt {{a^2} - {x^2}} }} = 0 \Leftrightarrow \left[ \begin{array}{l}x = - a \notin \left( {0 < x < a} \right)\\x = \frac{a}{2} \in \left( {0 < x < a} \right)\end{array} \right.\)
Bảng biến thiên hàm số \(f\left( x \right)\) trên khoảng \(\left( {0\,;\,a} \right)\)
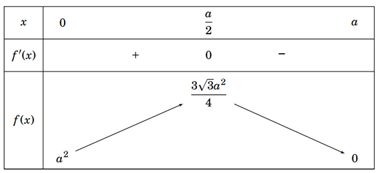
Từ bảng biến thiên suy ra \(\mathop {{\rm{max}}}\limits_{\left( {0;\,a} \right)} f\left( x \right) = f\left( {\frac{a}{2}} \right) = \frac{{3\sqrt 3 {a^2}}}{4}\)
Vậy bác nông dân có thể rào được mảnh vườn có diện tích lớn nhất là \(\frac{{3\sqrt 3 {a^2}}}{4}\)\({{\rm{m}}^2}\).
Lời giải
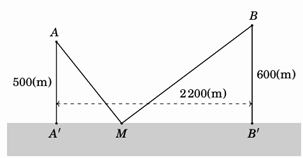
Đặt \(A'M = x\,\,\left( {0 < x < 2200} \right)\), \(B'M = 2200 - x\)
Ta có \(AM = \sqrt {{x^2} + {{500}^2}} \,,\,\,BM = \sqrt {{{\left( {2200 - x} \right)}^2} + {{600}^2}} \)
Khi đó tổng khoảng cách từ hai xã đến vị trí \(M\) là:
\(AM + BM = \sqrt {{x^2} + {{500}^2}} \, + \sqrt {{{\left( {2200 - x} \right)}^2} + {{600}^2}} \)
Xét hàm số \(f\left( x \right) = \sqrt {{x^2} + {{500}^2}} \, + \sqrt {{{\left( {2200 - x} \right)}^2} + {{600}^2}} \) trên khoảng \(\left( {0;\,2200} \right)\)
Đạo hàm \(f'\left( x \right) = \frac{x}{{\sqrt {{x^2} + {{500}^2}} }} - \frac{{2200 - x}}{{\sqrt {{{\left( {2200 - x} \right)}^2} + {{600}^2}} }} = 0 \Leftrightarrow x = 1000\)
Bảng biến thiên: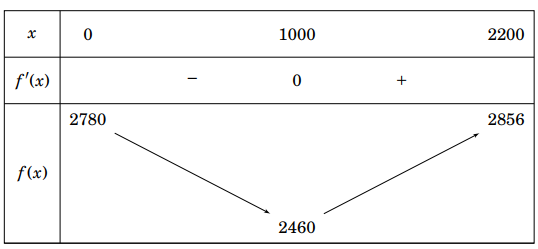
Lời giải
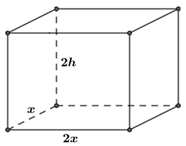
Gọi \(x\left( m \right)\) là chiều rộng. \((x > 0)\). Chiều dài là \(2x\left( m \right)\). Chiều cao là \(h\left( m \right)\). \(\left( {h > 0} \right)\)
Theo đề bài, ta có: \(2{x^2} + 4xh + 2xh = 5,5\)\( \Leftrightarrow 2{x^2} + 6xh = 5,5\)\( \Leftrightarrow h = \frac{{5,5 - 2{x^2}}}{{6x}}\)
Vì \(h > 0\)và \(x > 0\)nên \(5,5 - 2{x^2} > 0 \Leftrightarrow 0 < x < \frac{{\sqrt {11} }}{2}\).
Suy ra thể tích của bể cá là: \(V = 2{x^2}h = \frac{{5,5}}{3}x - \frac{2}{3}{x^3}\) với \(0 < x < \frac{{\sqrt {11} }}{2}\).
\(V' = \frac{{11}}{6} - 2{x^2}\)\( = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{\sqrt {33} }}{6}(N)\\x = - \frac{{\sqrt {33} }}{6}(L)\end{array} \right.\)
Thể tích lớn nhất của bể cá là: \({V_{max}} = V\left( {\frac{{\sqrt {33} }}{6}} \right) \approx 1,17\left( {{m^3}} \right)\).
Lời giải
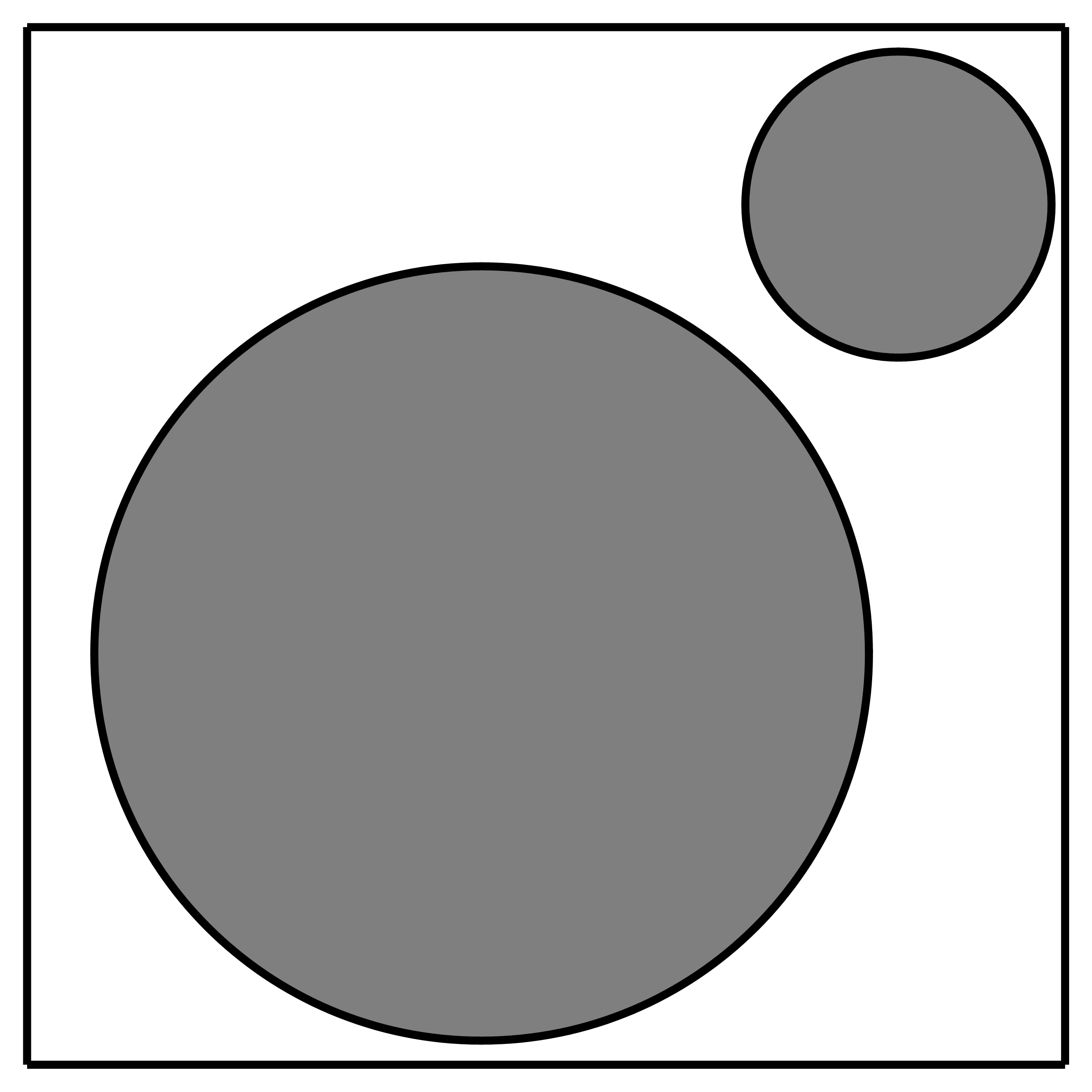
Gọi đường chéo hình chữ nhật là \(a\). Ta có: \[R + r = \frac{a}{{1 + \sqrt 2 }}\].
Tìm max của \[{R^2} + {r^2}\]. Khảo sát hàm, ta tìm được \[R = \frac{a}{{2\sqrt 2 }}\] Từ đó ta tìm được \(\sqrt k = \sqrt 2 - 1\).
Lời giải
Gọi \(x{\rm{ }}\left( {0 < x < 60} \right)\) là chiều dài của đoạn thứ hai, suy ra \(60 - x\) là độ dài đoạn thứ nhất.
Khi đó cạnh hình vuông là \(15 - \frac{x}{4}\) nên diện tích hình vuông là \({\left( {15 - \frac{x}{4}} \right)^2}\).
Chu vi của vòng tròn là \(2\pi R = x \Rightarrow R = \frac{x}{{2\pi }}\). Khi đó diện tích hình tròn là \(\pi {R^2} = \frac{{{x^2}}}{{4\pi }}\).
Khi đó tổng diện tích của hai hình sẽ là \(f\left( x \right) = \frac{{{x^2}}}{{4\pi }} + {\left( {15 - \frac{x}{4}} \right)^2}\).
Khi đó ta có \(f'\left( x \right) = \frac{x}{{2\pi }} - \frac{1}{2}\left( {15 - \frac{x}{4}} \right) = \frac{x}{2}\left( {\frac{1}{\pi } + \frac{1}{4}} \right) - \frac{{15}}{2}\).
Cho \(f'\left( x \right) = 0 \Rightarrow x = \frac{{15}}{{\frac{1}{\pi } + \frac{1}{4}}}\). Suy ra tổng diện tích hai hình nhỏ nhất khi \(x = \frac{{60\pi }}{{4 + \pi }}\).
Khi đó cạnh hình vuông sẽ là \(60 - \frac{{60\pi }}{{4 + \pi }} \approx 33,61\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.