10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải
395 người thi tuần này 4.6 1.2 K lượt thi 10 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: D
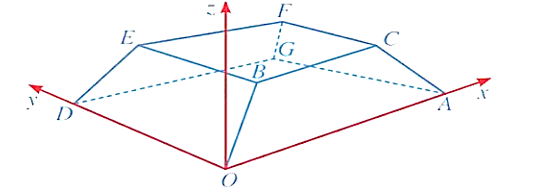
Vì B(3k; 2k; k) (CBEF): z = 3 nên k = 3.
Suy ra B(9; 6; 3). Khi đó a + b + c = 18.
Lời giải
Đáp án đúng là: D
Do mặt dưới của mái nhà thuộc mặt phẳng vuông góc với trục Oz và đi qua A(3; 4; 33) nên phương trình mặt phẳng chứa mặt dưới của mái nhà là: z – 33 = 0.
Khoảng cách từ điểm D đến mặt phẳng chứa mặt dưới của mái nhà bằng:
\(\frac{{\left| {35 - 33} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 2\).
Lời giải
Đáp án đúng là: B
Chọn hệ trục tọa độ như hình vẽ
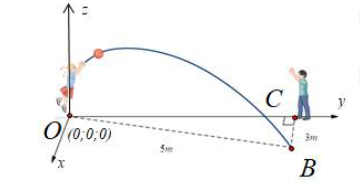
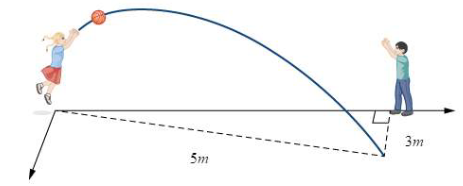
Ta có \(OC = \sqrt {O{B^2} - B{C^2}} = 4\). Suy ra B(3; 4; 0).
Mặt phẳng chứa quỹ đạo đi qua O(0; 0; 0) và nhận \(\overrightarrow k \left( {0;0;1} \right),\overrightarrow {OB} \left( {3;4;0} \right)\) làm vectơ chỉ phương.
Suy ra vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow k ,\overrightarrow {OB} } \right] = \left( { - 4;3;0} \right)\).
Vậy phương trình mặt phẳng chứa quỹ đạo của quả bóng là
−4(x – 0) + 3(y – 0) + 0(z – 0) = 0 4x – 3y = 0.
Do đó a + c = 4.
Câu 4
A. 2,58;
B. 2,85;
C. 3,85;
D. 3,58.
Lời giải
Đáp án đúng là: B
Ta có \(\overrightarrow {AB} = \left( {3;1;0} \right),\overrightarrow {AC} = \left( {6;2; - 1} \right)\).
Mặt phẳng (ABC) có vectơ pháp tuyến là \(\overrightarrow n = \left( { - 1;3;0} \right)\) nên phương trình (ABC):
x – 3y + 3 = 0.
Vậy khoảng cách \(d\left( {D,\left( {ABC} \right)} \right) = \frac{{\left| {1.6 + 3} \right|}}{{\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{9\sqrt {10} }}{{10}} \approx 2,85\).
Lời giải
Đáp án đúng là: A
Vì (Q) // (P) nên (Q) có một vectơ pháp tuyến là \(\overrightarrow n = \left( {6;5;1} \right)\).
Nên phương trình mặt phẳng (Q): 6x + 5y + z – 12 = 0.
Do đó A + B + C + D = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.