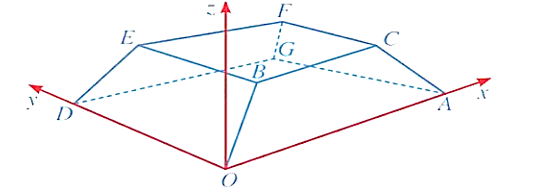
Hình dưới đây là hình ảnh minh họa của một tòa nhà trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục theo mét). Biết A(50; 0; 0), D(0; 20; 0), B(3k; 2k; k) với k > 0 và (CBEF) có phương trình z = 3. Biết rằng tọa độ điểm B(a; b; c). Khi đó giá trị a + b + c bằng bao nhiêu?
A. 9;
B. 6;
C. 3;
D. 18.
Quảng cáo
Trả lời:
Đáp án đúng là: D
Vì B(3k; 2k; k) (CBEF): z = 3 nên k = 3.
Suy ra B(9; 6; 3). Khi đó a + b + c = 18.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
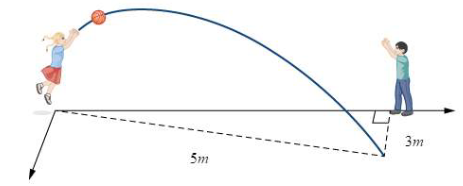
Gọi mặt phẳng (P) đi qua 3 điểm pháo A(3; 0; 0), B(0; 1,5; 0), C(0; 0; −1,5) nên có phương trình là \(\frac{x}{3} + \frac{y}{{1,5}} + \frac{z}{{ - 1,5}} = 1 \Leftrightarrow x + 2y - 2z - 3 = 0\).
Giả sử điểm G(xG; yG; zG) là vị trí khi mục tiêu bay tới mặt phẳng (P) để tới vị trí N nên G ∈ (P).
Do \(\overrightarrow {MG} ,\overrightarrow {MN} \) là 2 vectơ cùng hướng nên tồn tại số thực t > 0 sao cho \(\overrightarrow {MG} = t\overrightarrow {MN} \).
Ta có \(\overrightarrow {MG} = \left( {{x_G} - 5;{y_G} - 2;{z_G} - 4} \right);\overrightarrow {MN} = \left( { - 4; - 2; - 6} \right)\).
Nên \(\left\{ \begin{array}{l}{x_G} - 5 = - 4t\\{y_G} - 2 = - 2t\\{z_G} - 4 = - 6t\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}{x_G} = 5 - 4t\\{y_G} = 2 - 2t\\{z_G} = 4 - 6t\end{array} \right.\).
Vì G ∈ (P) 5 – 4t + 2(2 – 2t) – 2(4 – 6t) = 3 t = \(\frac{1}{2}\) G(3; 1; 1).
Do đó \(\overrightarrow {AG} = \left( {0;1;1} \right) \Rightarrow AG = \sqrt 2 \approx 1,41\).
Lời giải
Đáp án đúng là: B
Chọn hệ trục tọa độ như hình vẽ
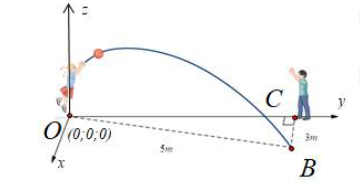
Ta có \(OC = \sqrt {O{B^2} - B{C^2}} = 4\). Suy ra B(3; 4; 0).
Mặt phẳng chứa quỹ đạo đi qua O(0; 0; 0) và nhận \(\overrightarrow k \left( {0;0;1} \right),\overrightarrow {OB} \left( {3;4;0} \right)\) làm vectơ chỉ phương.
Suy ra vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow k ,\overrightarrow {OB} } \right] = \left( { - 4;3;0} \right)\).
Vậy phương trình mặt phẳng chứa quỹ đạo của quả bóng là
−4(x – 0) + 3(y – 0) + 0(z – 0) = 0 4x – 3y = 0.
Do đó a + c = 4.
Câu 3
A. 2,58;
B. 2,85;
C. 3,85;
D. 3,58.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.