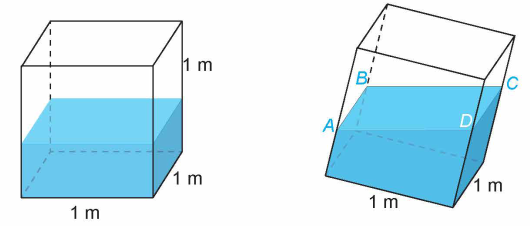
10 bài tập Một số dạng toán thực tế liên quan đến Công thức tính góc trong không gian (có lời giải)
43 người thi tuần này 4.6 239 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
Đường thẳng d và d' có vectơ chỉ phương lần lượt là \(\vec a = (2;1; - 1),\overrightarrow {{a^\prime }} = (3;3;9)\)
Ta có \(\cos \left( {d,{d^\prime }} \right) = \frac{{|2.3 + 1 \cdot 3 + ( - 1) \cdot 9|}}{{\sqrt {{2^2} + {1^2} + {1^2}} \cdot \sqrt {{3^2} + {3^2} + {9^2}} }} = \frac{0}{{3\sqrt {66} }} = 0\). Suy raLời giải
Đường thẳng d có vectơ chỉ phương là \(\vec a = (0;1;1)\)
Mặt phẳng \(({\rm{P}})\) có vectơ pháp tuyến là \(\vec n = (0;0;1)\)
\(\sin (d,(P)) = \frac{{|0.0 + 1.0 + 1 \cdot 1|}}{{\sqrt {{1^2} + {1^2}} \cdot \sqrt {{1^2}} }} = \frac{1}{{\sqrt 2 }}\). Suy raLời giải
Mặt phẳng \(({\rm{P}})\) có vectơ pháp tuyến \(\vec n = (4;0;11)\)
Mặt phẳng \(({\rm{Q}})\) có vectơ pháp tuyến \(\overrightarrow {{n^\prime }} = (0;0;1)\)
Có \(\cos ((P),(Q)) = \frac{{|4.0 + 0.0 + 11.1|}}{{\sqrt {{4^2} + {{11}^2}} \cdot \sqrt {{1^2}} }} = \frac{{11}}{{\sqrt {173} }}\). Suy raLời giải
a) Mặt phảng \(({\rm{P}})\) có vectơ pháp tuyến là \(\vec n = (2;0;2)\)
Mặt phắng \(\left( {{{\rm{P}}^\prime }} \right)\) có vectơ pháp tuyến là \(\overrightarrow {{n^\prime }} = (1;0;1)\)
\(\cos \left( {(P),\left( {{P^\prime }} \right)} \right) = \frac{{|2.1 + 0.0 + 2.1|}}{{\sqrt {{2^2} + {2^2}} \cdot \sqrt {{1^2} + {1^2}} }} = \frac{4}{4} = 1\). Suy ra ((P),(P’)) .
b) Mặt phẳng \((Q)\) có vectơ pháp tuyến là \(\overrightarrow {{n_Q}} = (0;0;1)\)
\(\cos ((P),(Q)) = \frac{{|2.0 + 0.0 + 2.1|}}{{\sqrt {{2^2} + {2^2}} \cdot \sqrt {{1^2}} }} = \frac{2}{{2\sqrt 2 }} = \frac{1}{{\sqrt 2 }}{\rm{. }}\) Suy ra ((P), (Q)) .
\(\cos \left( {\left( {{P^\prime }} \right),(Q)} \right) = \frac{{|1.0 + 0.0 + 1.1|}}{{\sqrt {{1^2} + {1^2}} \cdot \sqrt 1 }} = \frac{1}{{\sqrt 2 }}{\rm{. }}\)Suy ra .
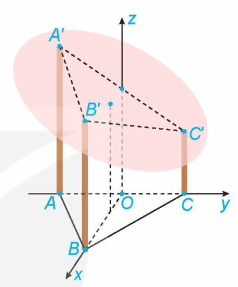
Mặt phắng ( \({{\rm{O}}^\prime }{\rm{BC}}\) ) có phương trình đoạn chắn là: \(\frac{x}{3} + \frac{y}{1} + \frac{z}{2} = 1 \Leftrightarrow 2{\rm{x}} + 6{\rm{y}} + 3{\rm{z}} = 6\) có vectơ pháp tuyến \(\vec n = (2;6;3)\)
\(\cos \left( {\left( {{O^\prime }BC} \right),(OBC)} \right) = \frac{{|3|}}{{\sqrt 1 \cdot \sqrt {{2^2} + {6^2} + {3^2}} }} = \frac{3}{7}\). Suy ra .
c) Đường thằng \({B^\prime }C\) nhận \(\overrightarrow {{B^\prime }C} = ( - 3;1; - 2)\) làm vectơ chỉ phương.
Mặt phẳng ( O ' BC ) có vectơ pháp tuyến \(\vec n = (2;6;3)\)
\(\sin \left( {{B^\prime }C,\left( {{O^\prime }BC} \right)} \right) = \frac{{|( - 3) \cdot 2 + 1 \cdot 6 + ( - 2) \cdot 3|}}{{\sqrt {{{( - 3)}^2} + {1^2} + {{( - 2)}^2}} \cdot \sqrt {{2^2} + {6^2} + {3^2}} }} = \frac{6}{{7\sqrt {14} }}\). Suy ra .
Lời giải
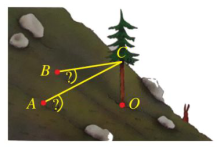
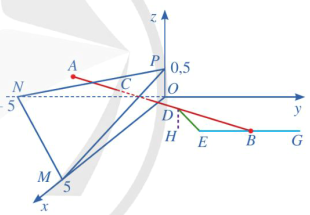
a) Do điểm \(C(0;0;5)\) nên \(AC = \sqrt {{{(3 - 0)}^2} + {{( - 4 - 0)}^2} + {{(2 - 5)}^2}} = \sqrt {34} (\;{\rm{m}})\);
\(BC = \sqrt {{{( - 5 - 0)}^2} + {{( - 2 - 0)}^2} + {{(1 - 5)}^2}} = \sqrt {45} = 3\sqrt 5 (\;{\rm{m}}){\rm{. }}\)
b) Ta có: \(\overrightarrow {OA} = (3; - 4;2),\overrightarrow {OB} = ( - 5; - 2;1)\) nên \([\overrightarrow {OA} ,\overrightarrow {OB} ] = \left( {\left| {\begin{array}{*{20}{l}}{ - 4}&2\\{ - 2}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}2&3\\1&{ - 5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}3&{ - 4}\\{ - 5}&{ - 2}\end{array}} \right|} \right) = (0; - 13; - 26){\rm{. }}\)
Vì thế, vectơ \(\vec n = (0;1;2)\) là một vectơ pháp tuyến của mặt phẳng \((OAB)\).
Mặt khác, do \(\overrightarrow {CA} = (3; - 4; - 3),\overrightarrow {BC} = (5;2;4)\) nên ta có:
- \(\sin (CA,(OAB)) = |\cos (\overrightarrow {CA} ,\vec n)| = \frac{{|\overrightarrow {CA} \cdot \vec n|}}{{|\overrightarrow {CA} | \cdot |\vec n|}} = \frac{{|3 \cdot 0 + ( - 4) \cdot 1 + ( - 3) \cdot 2|}}{{\sqrt {34} \cdot \sqrt 5 }} = \frac{{10}}{{\sqrt {170} }}\),
suy ra . Vậy góc tạo bởi dây neo CA và mặt phẳng sườn núi là khoảng .
\({\rm{ - }}\sin (BC,(OAB)) = |\cos (\overrightarrow {BC} ,\vec n)| = \frac{{|\overrightarrow {BC} \cdot \vec n|}}{{|\overrightarrow {BC} | \cdot |\vec n|}} = \frac{{|5 \cdot 0 + 2 \cdot 1 + 4 \cdot 2|}}{{3\sqrt 5 \cdot \sqrt 5 }} = \frac{2}{3}{\rm{, }}\)
suy ra . Vậy góc tạo bởi dây neo BC và mặt phẳng sườn núi là khoảng .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.