6 bài tập Tìm vectơ pháp tuyến – cặp vectơ chỉ phương (có lời giải)

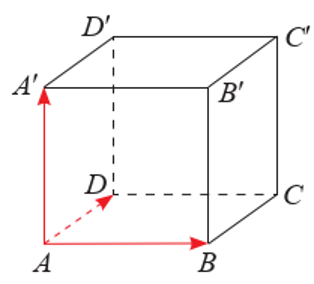
a) Vì \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) không cùng phương và có giá nằm trong mặt phẳng \((ABCD)\) nên \(\overrightarrow {AB} ,\overrightarrow {AD} \) là một cặp vectơ chỉ phương của \((ABCD)\).

b) Vì \(A{A^\prime } \bot (ABCD)\) nên \(\overrightarrow {A{A^\prime }} \) là một vectơ pháp tuyến của \((ABCD)\)

Một vectơ pháp tuyến của mặt phẳng \((P)\) là: \(\vec n = [\vec a,\vec b]{\rm{ }} = \left( {\left| {\begin{array}{*{20}{c}}3&5\\{ - 1}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}5&1\\1&{ - 3}\end{array}} \right|;{\rm{ }}\left| {{\mkern 1mu} \begin{array}{*{20}{c}}1&3\\{ - 3}&{ - 1}\end{array}} \right|} \right) = (8; - 16;8).\)

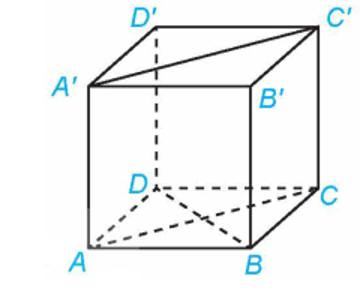
Ta có \(\overrightarrow {AB}  = (2;1; - 2),\overrightarrow {AC}  = ( - 12;6;0)\) nên \(\overrightarrow {AB} ,\overrightarrow {AC} \) không cùng phương. Mà chúng có giá nằm trong mặt phẳng \((ABC\) nên \(\overrightarrow {AB} ,\overrightarrow {AC} \) là một cặp vectơ chỉ phương của mặt phẳng \((ABC)\).

Vậy một vectơ pháp tuyến của \((ABC)\) là:

\(\vec n = [\overrightarrow {AB} ,\overrightarrow {AC} ] = \left( {\left| {\begin{array}{*{20}{r}}1&{ - 2}\\6&0\end{array}} \right|;\left| {\begin{array}{*{20}{r}}{ - 2}&2\\0&{ - 12}\end{array}} \right|;\left| {\begin{array}{*{20}{l}}2&1\\{ - 12}&6\end{array}} \right|} \right) = (1.0 - 6 \cdot ( - 2);( - 2).( - 12) - 0.2;2.6 - ( - 12).1) = (12;24;24)\) (Ta cũng có thể chọn vectơ \(\overrightarrow {{n^\prime }}  = \frac{1}{{12}}\vec n = (1;2;2)\) là một vectơ pháp tuyến của \((ABC)\) ).

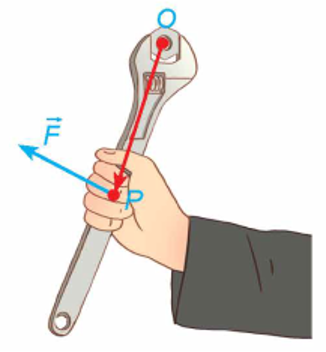
a) Ta có \(\quad \vec M = [\overrightarrow {OP} ,\vec F] = \left( {\left| {\begin{array}{*{20}{l}}y&z\\b&c\end{array}} \right|;\left| {\begin{array}{*{20}{l}}z&x\\c&a\end{array}} \right|;\left| {\begin{array}{*{20}{l}}x&y\\a&b\end{array}} \right|} \right)\) \( = (yc - bz;za - cx;bx - ay)\)

b) Vì \(\overrightarrow {O{P^\prime }}  = 2\overrightarrow {OP} \) nên \(2\overrightarrow {OP}  = (2x;2y;2z)\)

Khi đó \(\overrightarrow {{M^\prime }}  = \left[ {\overrightarrow {O{P^\prime }} ,\vec F} \right] = \left( {\left| {\begin{array}{*{20}{c}}{2y}&{2z}\\b&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2z}&{2x}\\c&a\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2x}&{2y}\\a&b\end{array}} \right|} \right){\rm{ }}\)\( = (2yc - b2z;2za - 2cx;2bx - 2ay)\)

Suy ra \(\overrightarrow {{M^\prime }}  = 2\vec M\).

Vậy giữ nguyên lực tác động \(\vec F\) trong khi thay vị trí đặt lực từ P sang \({{\rm{P}}^\prime }\) sao cho \(\overrightarrow {O{P^\prime }}  = 2\overrightarrow {OP} \) thì moment lực sẽ tăng lên gấp đôi.

Kết luận: Từ kết quả trên, ta có thể rút ra rằng để đỡ tốn sức khi dùng mỏ lết vặn ốc, ta nên tăng khoảng cách từ điểm tác dụng lực đến trục quay (điểm O ).

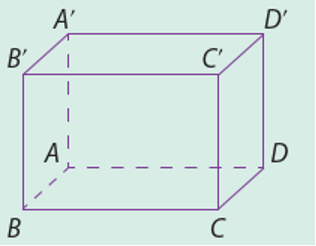
Vì các đường thẳng \(A{A^\prime },B{B^\prime }\) vuông góc với mặt phẳng \((ABCD)\) nên \(\overline {A{A^\prime }} ,2\overline {B{B^\prime }} \) đều là vectơ pháp tuyến của mặt phẳng \((ABCD)\).

Đường thẳng BD vuông góc với hai đường thẳng AC và \(A{A^\prime }\) nên vuông góc với mặt phẳng \(\left( {AC} \right.C'A')\). Vậy \(\overrightarrow {BD} \) là một vectơ pháp tuyến của mặt phẳng ( \(AC{C^\prime }A\) ).

Đường thẳng \({A^\prime }{C^\prime }\) không vuông góc với mặt phẳng \((ABCD)\) nên vectơ \(\overline {{A^\prime }{C^\prime }} \) không phải là vectơ pháp tuyến của mặt phẳng đó.

Vậy các khẳng định a và b là đúng, khẳng định c là sai.

Bốn vectơ pháp tuyến của mặt phẳng \(\left( {A{A^\prime }{B^\prime }B} \right)\) là: \(\overrightarrow {AD} ,\overrightarrow {{A^\prime }{D^\prime }} ,\overrightarrow {BC} ,\overrightarrow {{B^\prime }{C^\prime }} \). Hai cặp vectơ chỉ phương của mặt phẳng \(\left( {A{A^\prime }{B^\prime }B} \right)\) là: \(\overrightarrow {AB} ,\overrightarrow {A{A^\prime }} \) và \(\overrightarrow {AB} ,\overrightarrow {A{B^\prime }} \).