Đề kiểm tra Ứng dụng hình học của tích phân (có lời giải) - Đề 1
4.6 0 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 1
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 9
Danh sách câu hỏi:
Câu 1
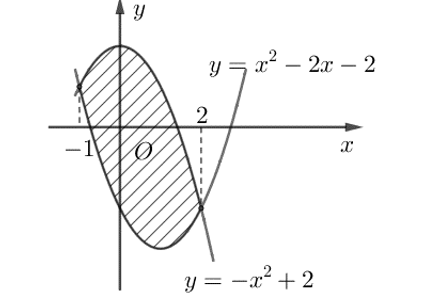
A. \[\int_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \].
B. \[\int_{ - 1}^2 {\left( {2{x^2} - 2x - 4} \right)dx} \].
Lời giải
Chọn A
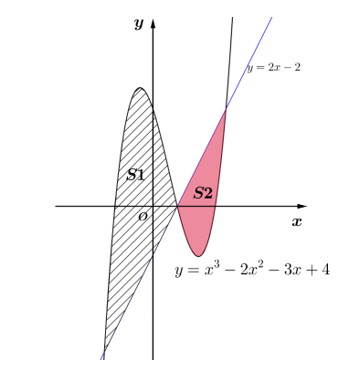
Dựa và hình vẽ ta có diện tích hình phẳng được gạch chéo trong hình bên là:
\(\int_{ - 1}^2 {\left[ {\left( { - {x^2} + 2} \right) - \left( {{x^2} - 2x - 2} \right)} \right]{\rm{d}}x} = \int_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right){\rm{d}}x} .\)Câu 2
A. \(V = \int\limits_a^b {\left| {f\left( x \right)} \right|} dx\).
B. \(V = \pi \int\limits_a^b {{f^2}\left( x \right)} dx\).
Lời giải
Chọn B
Công thức tính thể tích \(V\) của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục \(Ox\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\), xung quanh trục \(Ox\) là \(V = \pi \int\limits_a^b {{f^2}\left( x \right)} dx\).Câu 3
Lời giải
Chọn A
Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường \[y = f\left( x \right),\;y = 0,\;\] \[x = a,\;x = b\] quanh trục \[Ox\] được tính theo công thứcCâu 4
Lời giải
Chọn B
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = {e^x},\] trục hoành và hai đường thẳng \[x = 0\] và \[x = 3\] làCâu 5
Lời giải
Chọn B
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\); \(y = x\) và hai đường thẳng \(x = 2;x = 3\) là
\[\begin{array}{l}S = \int\limits_2^3 {\left| {\frac{{{x^2} - 2x + 3}}{{x - 1}} - x} \right|dx = } \int\limits_2^3 {\left| {\frac{{ - x + 3}}{{x - 1}}} \right|dx = } \int\limits_2^3 {\left| { - 1 + \frac{2}{{x - 1}}} \right|dx = } \\ = \left( { - x + 2\ln \left| {x - 1} \right|} \right)\mathop |\nolimits_2^3 = \left( { - 3 + 2\ln 2} \right) + 2 = - 1 + 2\ln 2\end{array}\]
Vậy \(a = 2;b = - 1 \Rightarrow a + b = 1\).Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
a) Diện tích hình học phẳng được giới hạn bới hàm số đã cho, trục hoành, \(x = - 1\)và \(x = 1\) là \(\frac{{{e^2} - 1}}{e}\).
b) Với \(a = \ln 4\) thì diện tích hình học phẳng được giới hạn bới hàm số đã cho, các trục tọa độ và đường thẳng \(x = a\) bằng \(3\).
c) Cho hình phẳng \[D\] giới hạn bởi đường cong \[y = {e^x},\] trục hoành và các đường thẳng \[x = 0,\]\[x = 1.\] Khối tròn xoay tạo thành khi quay \[D\] quanh trục hoành có thể tích \(V\) bằng \[V = 2\pi \left( {{e^2} - 1} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
a) Đường thẳng \(d\) cắt đồ thị \(\left( C \right)\) tại ba điểm \(A\left( { - 2; - 6} \right),\,B\left( {1;0} \right),\,C\left( {3;4} \right)\).
b) Diện tích hình phẳng giới hạn bởi đồ thị \(\left( C \right)\), trục hoành, đường thẳng \(x = - 1;\,x = 2\)bằng \(\frac{{21}}{4}\).
c) Diện tích hình phẳng giới hạn bởi đồ thị \(\left( C \right)\) và đường thẳng \(d\) bằng \(\frac{{253}}{{12}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
a) Diện tích hình phẳng \(D\) giới hạn bởi đồ thị hàm số \(y = \sqrt {x + 2} \,\,\,(x \ge - 2)\) , trục tung, trục hoành và đường thẳng \(x = 2\) là \({S_D} = \frac{{16}}{3} - \frac{{4\sqrt 2 }}{3}\,\)(đvdt).
b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {x + 2} \)và đường thẳng \(y = x\), hai đường thẳng \(x = 0\), \(x = 2\) là \(S = \frac{{10}}{3} - \frac{{2\sqrt 2 }}{9}\) (đvdt).
c) Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đường thẳng \(y = x\), trục hoành, hai đường thẳng \(x = 1\), \(x = 3\) quanh trục \[Ox\] là \(5\pi \) (đvtt).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
a) Diện tích hình phẳng \(D\) giới hạn bởi đồ thị hàm số \(\left( C \right)\), trục tung, trục hoành là \(\frac{3}{2} - 2\ln 2.\)
b) Diện tích hình phẳng \(H\) giới hạn bởi đồ thị hàm số \(\left( C \right)\), đường thẳng \(d\), \(x = 1\,,\,\,x = 2\) là \(\frac{5}{2} + 2\ln \frac{3}{2}\).
c) Thể tích của khối tròn xoay tạo thành khi quay hình phẳng \(D\) quanh trục \(Ox\) là \[\left( {\frac{{20}}{3} - 12\ln 2} \right)\pi \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số y = f(x) liên tục trên [ a; b ] có đồ thị như hình vẽ. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/02/blobid2-1769935394.png)