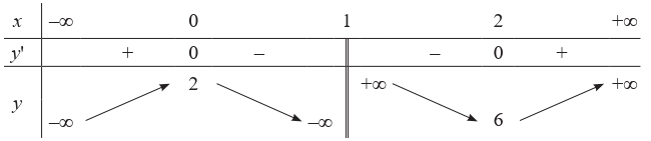
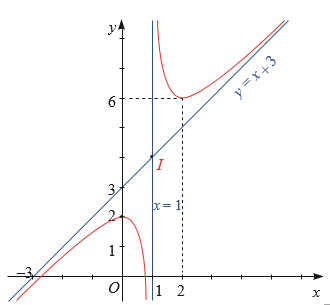
2 bài tập Khảo sát và vẽ đồ thị hàm số y = ax^2+bx+c/mx+n (a ≠ 0, m ≠ 0, đa thức tử không chia hết cho đa thức mẫu) (có lời giải)
33 người thi tuần này 4.6 317 lượt thi 1 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.