Quảng cáo
Trả lời:
Giải bởi Vietjack
|
1. Tập xác định: D = \[\mathbb{R}\] \ {1}. |
|
2. Sự biến thiên: |
|
• Chiều biến thiên: |
|
Đạo hàm \[y' = \frac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}}\]. Ta có y' = 0 ⇔ x = 0 hoặc x = 2. |
|
Trên các khoảng (−∞; 0) và (2; +∞), y' > 0 nên hàm số đồng biến trên mỗi khoảng đó. |
|
Trên các khoảng (0; 1) và (1; 2), y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó. |
|
Cực trị: |
|
Hàm số đạt cực tiểu tại x = 2 và yCT = 6. |
|
Hàm số đạt cực đại tại x = 0 và yCĐ = 2. |
|
Các giới hạn tại vô cực và tiệm cận: |
|
Ta có: \[\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = + \infty \] |
|
Ta có: \[a = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} + 2x - 2}}{{{x^2} - x}} = 1\] và \[b = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{{x^2} + 2x - 2}}{{x - 1}} - x} \right) = 3\]. Suy ra đường thẳng y = x + 3 là tiệm cận xiên của đồ thị hàm số. |
|
Ta có \[\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty \]. Suy ra đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số. |
|
Bảng biến thiên: 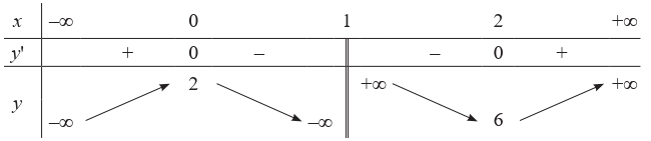 3. Đồ thị:
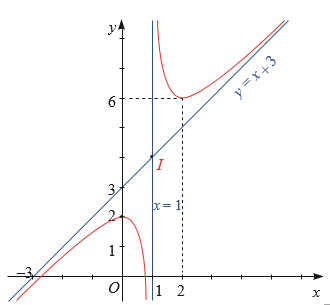 Ta có y = 0 ⇔ x2 + 2x – 2 = 0 ⇔ \[x = - 1 + \sqrt 3 \]hoặc \[x = - 1 - \sqrt 3 \]. Vậy đồ thị hàm số giao với trục Ox tại điểm (\[ - 1 + \sqrt 3 \];0) và điểm (\[ - 1 - \sqrt 3 \];0). Đồ thị hàm số giao với trục Oy tại điểm (0; 2). Đồ thị hàm số được biểu diễn trên Hình vẽ. Tâm đối xứng của đồ thị hàm số là điểm I(1; 4). Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 1 và y = x + 3. |
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập