10 bài tập Một số bài toán thực tế ứng dụng giá trị lớn nhất và giá trị nhỏ nhất của hàm có lời giải
47 người thi tuần này 4.6 238 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. t = 2;
B. t = 1;
C. t = 3;
D. t = 4.
Lời giải
Đáp án đúng là: B
Ta có v(t) = S'(t) = −3t2 + 6t = −3(t2 – 2t + 1) + 3 = −3(t – 1)2 + 3 ≤ 3.
Dấu “=” xảy ra khi t = 1.
Vậy vận tốc của chuyển động đạt giá trị lớn nhất bằng 3 khi t = 1.
Câu 2
A. 243 (m/s);
B. 27 (m/s);
C. 144 (m/s);
D. 36 (m/s).
Lời giải
Đáp án đúng là: D
Ta có: v = s' = −t2 + 12t; v' = −2t + 12; v' = 0 t = 6.
Bảng biến thiên
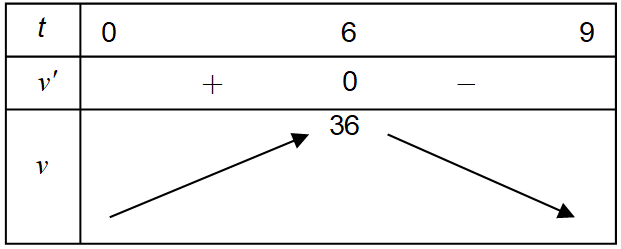
Nhìn bảng biến thiên ta thấy vận tốc đạt giá trị lớn nhất khi t = 6.
Giá trị lớn nhất là v(6) = 36 m/s.
Câu 3
A. 88 m/s;
B. 25 m/s;
C. 100 m/s;
D. 11 m/s.
Lời giải
Đáp án đúng là: B
Ta có v = S' = −t2 + 8t + 9, t ∈ (0; 10).
Có v' = −2t + 8; v' = 0 t = 4 ∈ (0; 10).
Bảng biến thiên:
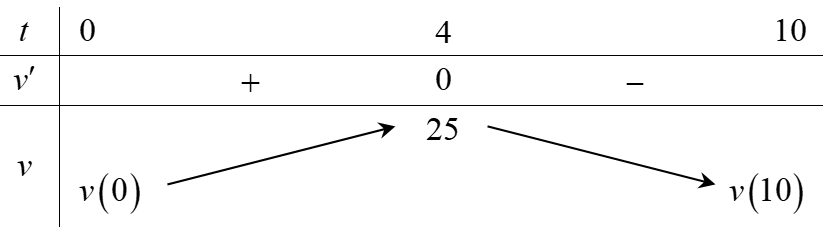
Vậy vận tốc lớn nhất của chất điểm là 25 m/s tại t = 4.
Câu 4
A. \(16\sqrt 3 \) cm;
B. \(4\sqrt 3 \)cm;
C. 24 cm;
D. \(8\sqrt 3 \)cm.
Lời giải
Đáp án đúng là: A
Gọi cạnh của hình chữ nhật: a, b; 0 < a, b 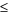 48
48
Ta có: \(ab = 48 \Leftrightarrow b = \frac{{48}}{a}\). Chu vi: \(P\left( a \right) = 2\left( {a + \frac{{48}}{a}} \right)\).
Có \[P'\left( a \right) = 2\left( {1 - \frac{{48}}{{{a^2}}}} \right);P'\left( a \right) = 0 \Leftrightarrow a = 4\sqrt 3 \].
Bảng biến thiên:
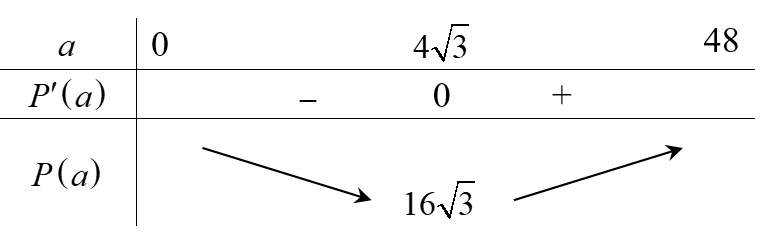
Vậy hình chữ nhật có chu vi nhỏ nhất là \(16\sqrt 3 \).
Câu 5
A. 3 cm;
B. 4 cm;
C. 5 cm;
D. 2 cm.
Lời giải
Đáp án đúng là: A
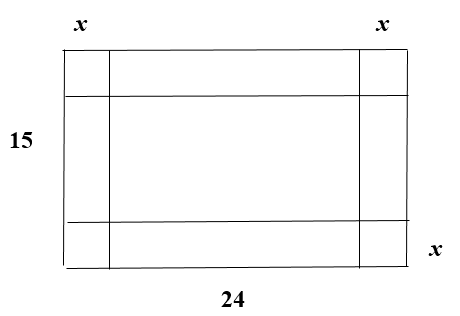
Giả sử độ dài cạnh hình vuông của các miếng tôn bị cắt bỏ bằng
x (\[0 < x < \frac{{15}}{2}\]).
Khi đó hình hộp chữ nhật có chiều cao bằng x, chiều rộng bằng 15 – 2x và chiều dài bằng 24 – 2x.
Suy ra hình hộp chữ nhật có thể tích V = x(15 – 2x)(24 – 2x) = 4x3 – 78x2 + 360x.
Xét hàm f(x) = 4x3 – 78x2 + 360x trên \[\left( {0;\frac{{15}}{2}} \right)\].
Có f'(x) = 12x2 – 156x + 360 = 0 x = 3 hoặc x = 10.
Bảng biến thiên
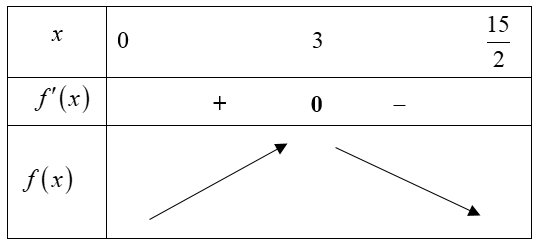
Dựa vào bảng biến thiên ta có hàm số đạt giá trị lớn nhất trên \[\left( {0;\frac{{15}}{2}} \right)\] tại x = 3 hay hình hộp chữ nhật có thể tích lớn nhất khi độ dài cạnh hình vuông của miếng tôn bị cắt bỏ bằng 3 cm.
Câu 6
A. 83200 đồng;
B. 320000 đồng;
C. 832000 đồng;
D. 32000 đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 4 giờ;
B. 1 giờ;
C. 3 giờ;
D. 2 giờ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.