6 bài tập Đọc đồ thị cho trước để tìm khoảng đơn điệu, cực trị (có lời giải)

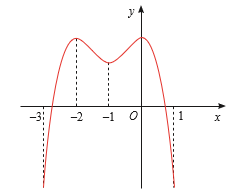
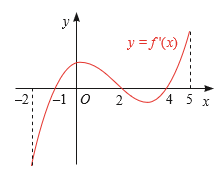
Hàm số đồng biến trên các khoảng (-3;-2) và (-1;0) Hàm số nghịch biến trên khoảng (-2;-1) và (0;1)

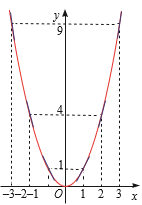
a) Hàm số đồng biến trên khoảng \((0; + \infty )\); Hàm số nghịch biến trên khoảng \(( - \infty ;0)\)

b) \({{\rm{f}}^\prime }({\rm{x}}) = {\left( {{x^2}} \right)^\prime } = 2{\rm{x}}\). Ta có: \({{\rm{f}}^\prime }({\rm{x}}) > 0 \Leftrightarrow 2x > 0 \Leftrightarrow x > 0\); \({{\rm{f}}^\prime }({\rm{x}}) < 0 \Leftrightarrow 2x < 0 \Leftrightarrow x < 0\)

c) Nhận xét:

\({{\rm{f}}^\prime }({\rm{x}}) > 0\) trên \(K\) thì \(y = f(x)\) đồng biến trên \(K\)

\({{\rm{f}}^\prime }({\rm{x}}) < 0\) trên \({\rm{K}}\) thì \({\rm{y}} = {\rm{f}}({\rm{x}})\) nghịch biến trên \({\rm{K}}\)

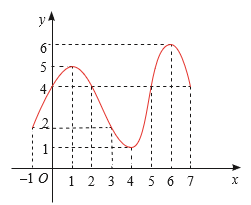
Hàm số y = f (x) có:

x = 1 là điểm cực đại vì f (x) < f (1) với mọi x ∈ (0; 2) \ {1}, y_cđ = f (1) = 5;

x = 6 là điểm cực đại vì f (x) < f (6) với mọi x ∈ (5; 7) \ {6}, y_cđ = f (6) = 6;

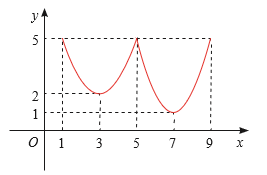
Hàm số \({\bf{y}} = {\bf{f}}({\bf{x}})\) có:

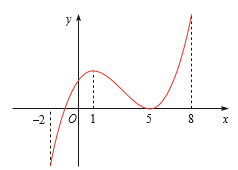
\({\rm{x}} = 5\) là điểm cực đại vì \({\rm{f}}({\rm{x}}) < {\rm{f}}(5)\) với mọi \(x \in (3;7)\backslash \{ 5\} ,{y_{cd}} = f(5) = 5\)

\({\rm{x}} = 3\) là điểm cực tiểu vì \({\rm{f}}({\rm{x}}) > {\rm{f}}(3)\) với mọi \(x \in (1;5)\backslash \{ 3\} ,{y_{ct}} = f(3) = 2\)

\({\rm{x}} = 7\) là diểm cực tiểu vì \({\rm{f}}({\rm{x}}) > {\rm{f}}(7)\) với mọi \(x \in (5;9)\backslash \{ 7\} ,{y_{ct}} = f(7) = 1\)