6 bài tập Tích của một số với một vectơ (có lời giải)
36 người thi tuần này 4.6 429 lượt thi 6 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
10000 câu trắc nghiệm tổng hợp Toán 2026 có đáp án - Phần 3
Trắc nghiệm Công thức xác suất toàn phần và công thức Bayes lớp 12 (có đáp án - phần 2)
Trắc nghiệm Công thức xác suất toàn phần và công thức Bayes lớp 12 (có đúng sai, trả lời ngắn)
Trắc nghiệm Xác suất có điều kiện lớp 12 (có đáp án - phần 2)
Trắc nghiệm Xác suất có điều kiện lớp 12 (có đúng sai, trả lời ngắn)
Trắc nghiệm Phương trình mặt cầu lớp 12 (có đáp án - phần 4)
Trắc nghiệm Phương trình mặt cầu lớp 12 (có đáp án - phần 3)
Trắc nghiệm Phương trình mặt cầu lớp 12 (có đáp án - phần 2)
Danh sách câu hỏi:
Lời giải
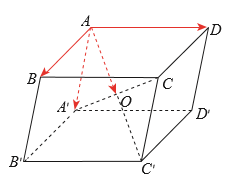
a) Theo quy tắc hình hộp ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A^\prime }} = \overrightarrow {A{C^\prime }} \).
\({\rm{b}})\) Vì \(A{A^\prime }//C{C^\prime }\) và \(A{A^\prime } = C{C^\prime }\) (vì cùng song song và bằng \(B{B^\prime }\) )
Nên \(A{A^\prime }{C^\prime }C\) là hình bình hành.
Mà \(A{C^\prime }\) và \({{\rm{A}}^\prime }C\) cắt nhau tại \({\rm{O}}\) nên \({\rm{O}}\) là trung điếm của \({\rm{AC}}\) '.
Suy ra \(AO = \frac{1}{2}A{C^\prime }\) mà \(\overrightarrow {AO} \) và \(\overrightarrow {A{C^\prime }} \) cùng hướng nên \(\overrightarrow {AO} = \frac{1}{2}\overrightarrow {A{C^\prime }} \) hay \(\overrightarrow {A{C^\prime }} = 2\overrightarrow {AO} \).
Lời giải
a) Ta có: \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN} ,\overrightarrow {MN} = \overrightarrow {MD} + \overrightarrow {DC} + \overrightarrow {CN} \).
Do đó \(2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {MD} + \overrightarrow {AB} + \overrightarrow {DC} + \overrightarrow {BN} + \overrightarrow {CN} \).
Vì \(M\) là trung điểm của đoạn thẳng AD nên \(\overrightarrow {MA} + \overrightarrow {MD} = \vec 0\).
Vì \(N\) là trung diểm của đoạn thẳng BC nên \(\overrightarrow {BN} + \overrightarrow {CN} = \vec 0\).
Do đó \(\overrightarrow {MN} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {DC} )\).
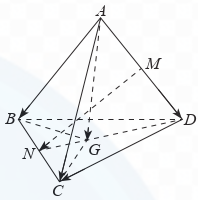
b) Ta có: \(\overrightarrow {AB} = \overrightarrow {AG} + \overrightarrow {GB} ,\overrightarrow {AC} = \overrightarrow {AG} + \overrightarrow {GC} ,\overrightarrow {AD} = \overrightarrow {AG} + \overrightarrow {GD} \).
Suy ra \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} \).
Vì \(G\) là trọng tâm của tam giác BCD nên \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0\).
Do đó \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
Lời giải
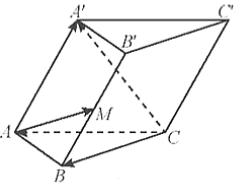
Vì \({\rm{M}}\) là trung diếm của \({\rm{BB}}\) nên \(\overrightarrow {BM} = \frac{1}{2}\overrightarrow {B{B^\prime }} \).
Do \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) là lăng trụ nên \(\overrightarrow {B{B^\prime }} = \overrightarrow {C{C^\prime }} \).
Có \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AC} + \overrightarrow {CB} + \frac{1}{2}\overrightarrow {B{B^\prime }} = \overrightarrow {CB} - \overrightarrow {CA} + \frac{1}{2}\overrightarrow {B{B^\prime }} = \vec b - \vec a + \frac{1}{2}\vec c\).
Lời giải
Lời giải
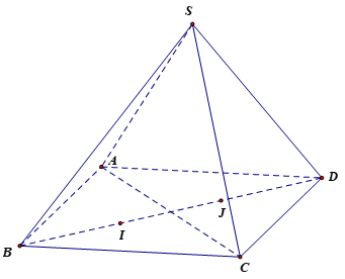
Vì \({\rm{I}}\) là trọng tâm của \({\rm{DABC}}\) nên \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \vec 0\)
\( \Leftrightarrow \overrightarrow {SA} - \overrightarrow {SI} + \overrightarrow {SB} - \overrightarrow {SI} + \overrightarrow {SC} - \overrightarrow {SI} = \vec 0 \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SI} (1).\)Tương tự, \(\overrightarrow {SA} + \overrightarrow {SD} + \overrightarrow {SC} = 3\overrightarrow {SJ} \) (2).
Cộng từng vế (1) và (2), ta có: \(2\overrightarrow {SA} + \overrightarrow {SB} + 2\overrightarrow {SC} + \overrightarrow {SD} = 3(SI + \overrightarrow {SJ} )\).
Lời giải
Khi ABCD.EFGH là hình hộp đứng thì EAC là tam giác vuông tại A, do đó:
EC2 = EA2 + AC2 = 100 + 91 = 191. Suy ra EM = \[EM = \frac{1}{3}\sqrt {191} \].
Nhắn tin Zalo
Hỏi bài tập