12 bài tập Khảo sát sự biến thiên và vẽ đồ thị của hàm số có lời giải
40 người thi tuần này 4.6 207 lượt thi 12 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải:
1) Tập xác định: ℝ.
2) Sự biến thiên
Ta có y' = 3x2 – 6x; y' = 0 3x2 – 6x = 0 x = 0 hoặc x = 2.
Hàm số đồng biến trên mỗi khoảng (−∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại x = 0; yCĐ = 4 ; hàm số đạt cực tiểu tại x = 2; yCT = 0.
Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \).
Bảng biến thiên:
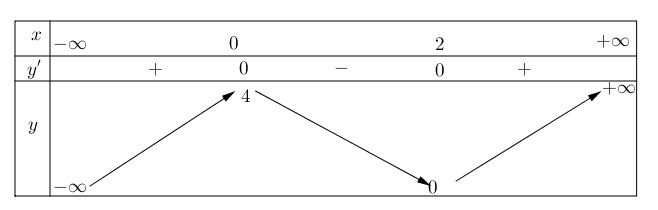
3) Đồ thị
- Giao điểm của đồ thị với trục tung: (0; 4).
- Giao điểm của đồ thị với trục hoành:
Xét phương trình x3 – 3x2 + 4 = 0 x = −1 hoặc x = 2.
Vậy đồ thị hàm số giao với trục hoành tại hai điểm (−1; 0) và (2; 0).
- Đồ thị hàm số đi qua các điểm (−1; 0), (2; 0), (0; 4) và (1; 2).
Vậy đồ thị hàm số y = x3 – 3x2 + 4 được cho ở Hình.
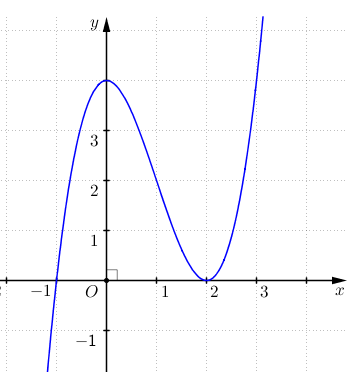
Quan sát đồ thị ở Hình, ta thấy đồ thị đó có tâm đối xứng là điểm I(1; 2).
Lời giải
Hướng dẫn giải:
1) Tập xác định: ℝ\{1}.
2) Sự biến thiên
\(y' = \frac{{ - 3}}{{{{(x - 1)}^2}}} < 0\) với mọi x ≠ 1.
Hàm số nghịch biến trên mỗi khoảng (−∞; 1) và (1; +∞).
Hàm số không có cực trị.
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\(\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty ,\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty \). Do đó, đường thẳng x = 1 là tiệm cận đứng của đổ thị hàm số.\(\mathop {\lim }\limits_{x \to + \infty } y = 2,\mathop {\lim }\limits_{x \to - \infty } y = 2\). Do đó, đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
Bảng biến thiên:
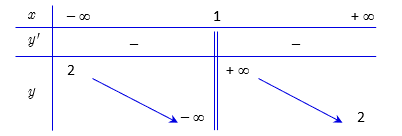
3) Đồ thị
- Giao điểm của đồ thị với trục tung: (0; −1).
- Giao điểm của đồ thị với trục hoành: \(\left( { - \frac{1}{2};0} \right)\).
Đồ thị hàm số đi qua các điểm \(( - 2;1),(2;5),\left( {\frac{5}{2};4} \right)\) và (4; 3).
Vậy đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 1}}\) được cho ở Hình.
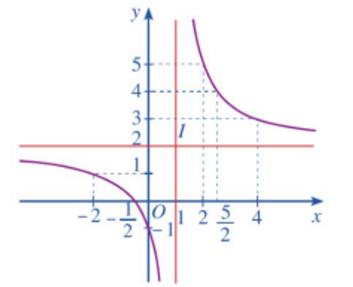
Quan sát đồ thị ở Hình, đồ thị đó nhận giao điểm I(1; 2) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Câu 3
A. 0;
B. 1;
C. 2;
D. −2.
Lời giải
Đáp án đúng là: C
Gọi M(x0; y0) là giao điểm của đồ thị hàm số với trục tung.
Ta có x0 = 0 y0 = 2.
Lời giải
Đáp án đúng là: A
Tập xác định: ℝ.
Ta có: y' = 3x2 – 3 = 3(x2 – 1); y' = 0 x = ± 1.
Bảng biến thiên
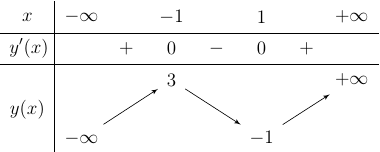
Từ bảng biến thiên ta thấy đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
Câu 5
A. (C) cắt trục hoành tại hai điểm;
B. (C) cắt trục hoành tại một điểm;
C. (C) không cắt trục hoành;
D. (C) cắt trục hoành tại ba điểm.
Lời giải
Đáp án đúng là: B
Phương trình hoành độ giao điểm của (C) và trục hoành là:
(x – 3)(x2 + 2) = 0 x = 3 nghĩa là (C) cắt trục hoành tại một điểm.
Câu 6
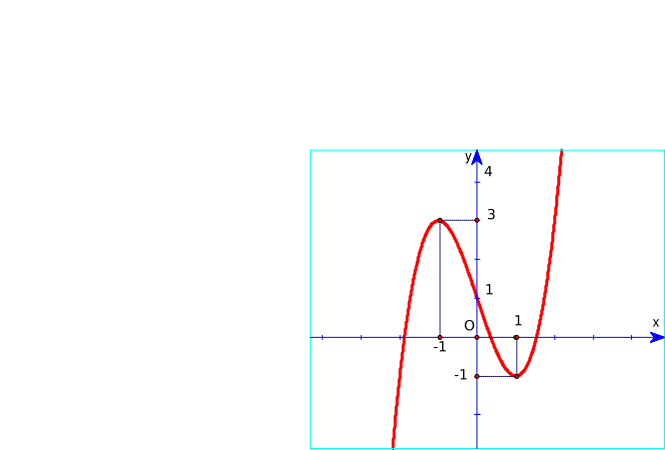
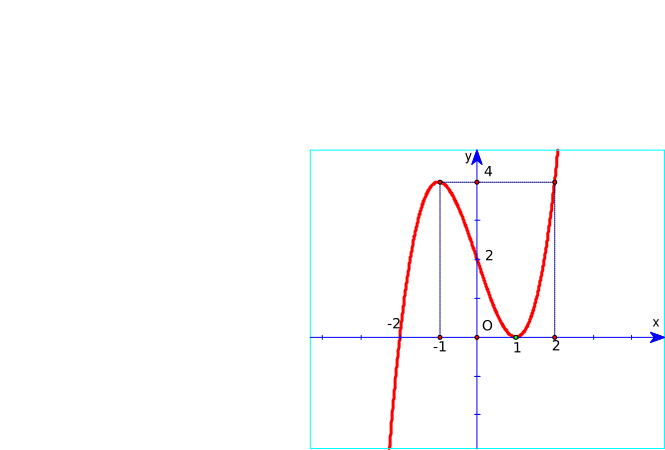
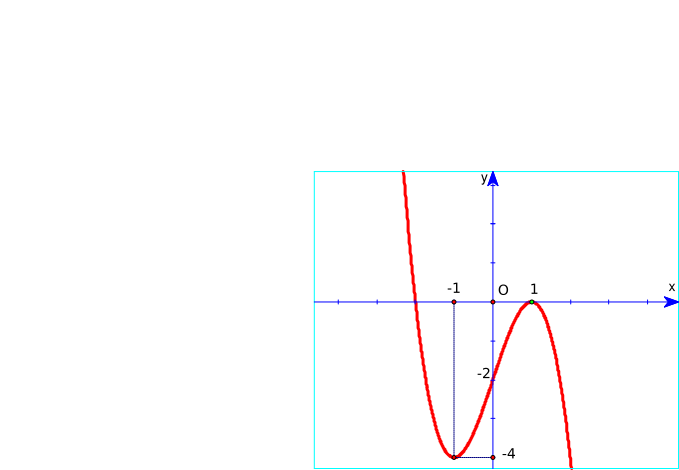
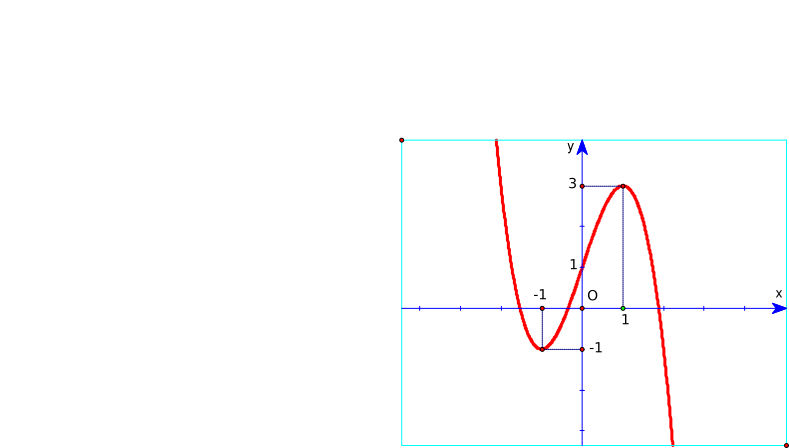
Đồ thị hàm số y = x3 – 3x + 2 là hình nào trong 4 hình dưới đây?
|
|
|
|
Hình 1 | Hình 2 | Hình 3 | Hình 4 |
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Hàm số y = −x3 + 3x2 – 1 là đồ thị nào sau đây?
|
|
|
|
Hình 1 | Hình 2 | Hình 3 | Hình 4 |
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
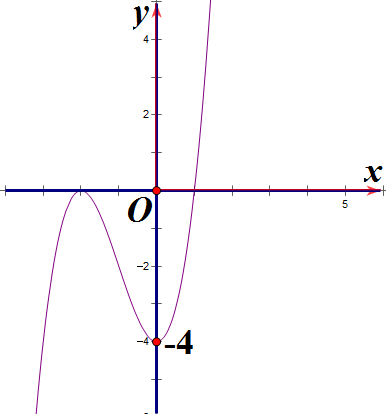
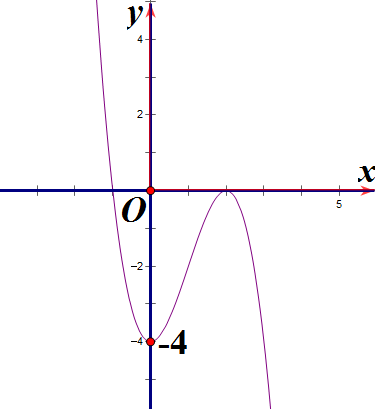
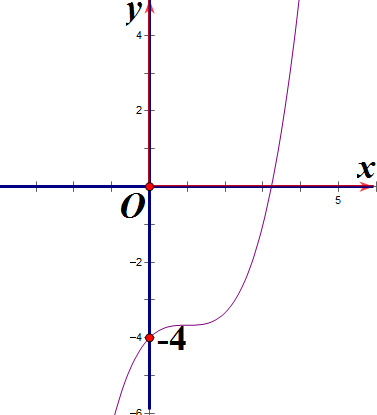
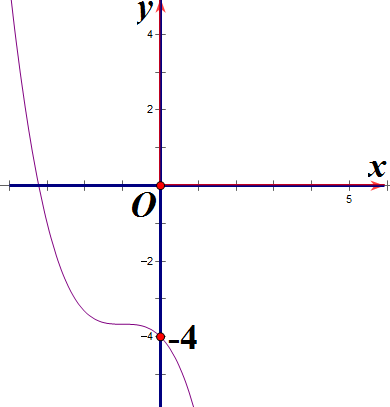
Hàm số y = x3 + 3x2 – 4 có đồ thị là hình nào sau đây?
|
|
|
|
Hình 1 | Hình 2 | Hình 3 | Hình 4 |
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
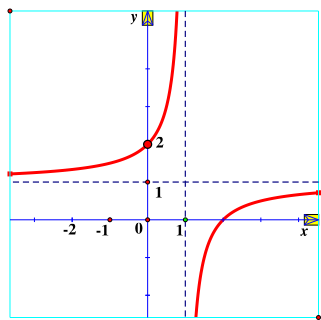
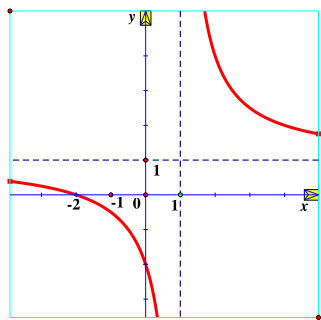
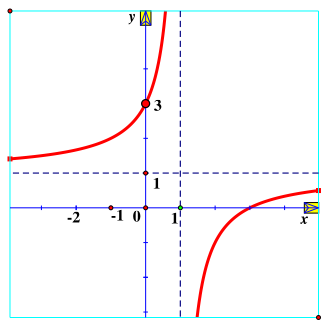
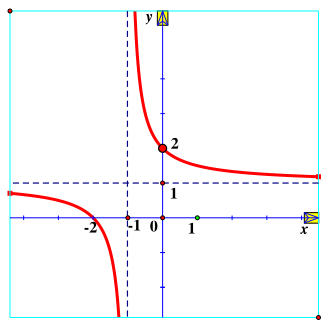
Hàm số \(y = \frac{{x - 2}}{{x - 1}}\) có đồ thị là hình vẽ nào sau đây?
|
|
|
|
|
|
|
|
Hình 1 |
Hình 2 | Hình 3 | Hình 4 |
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. Tập xác định của hàm số f(x) là D = ℝ\{−1};
B. Hàm số f(x) nghịch biến trên từng khoảng xác định của nó;
C. Đường thẳng y = x + 3 là đường tiệm cận xiên của (C);
D. Điểm I(−1; −1) là tâm đối xứng của đồ thị hàm số.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. Tâm đối xứng là I(1; 3);
B. Tiệm cận đứng là đường thẳng x = 1;
C. Tiệm cận xiên là đường thẳng y = x + 3;
D. Đồ thị hàm số đi qua điểm A(2; 6).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. Đồ thị hàm số (C) nhận đường thẳng x = 2 là tiệm cận ngang;
B. Đồ thị hàm số (C) nhận I(2; 3) là tâm đối xứng;
C. Tiếp tuyến của (C) tại giao điểm của (C) với Oy có phương trình y = −5x – 3;
D. Tích khoảng cách từ một điểm bất kỳ trên (C) tới 2 đường tiệm cận của nó luôn bằng 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.