20 bài tập Một số bài toán thực tế liên quan đến nguyên hàm (có lời giải)
59 người thi tuần này 4.6 318 lượt thi 20 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
a) Gọi h(t) là độ cao của quả bóng tại thời điểm t (h(t) tính theo mét, t tính theo giây).
Khi đó, ta có: h(t) = \[\int {\left( { - 9,8t + 19,6} \right)dt} \] = -4,9t2 +19,6t+C.
Mà quả bóng được ném lên từ độ cao 24,5 m tức là tại thời điểm t = 0 thì h = 24,5 hay h(0) = 24,5.
Suy ra C = 24,5.
Vậy công thức tính độ cao h (t) của quả bóng theo thời gian là: h(t)=-4,9t2 +19,6t +24,5.
b) Khi quả bóng chạm đất thì h(t) = 0. Ta có: – 4,9t2 + 19,6t + 24,5 = 0. Giải phương trình ta được:
t = - l; t =5. Mà t > 0 nên t = 5. Vậy sau 5 giây kể từ khi được ném lên thì quả bóng chạm đất.
Lời giải
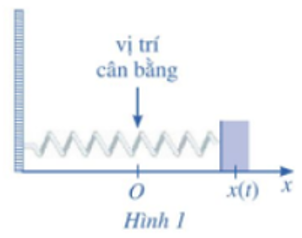
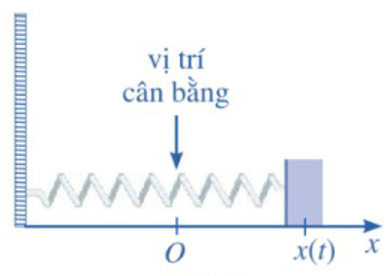
Giả sử con lắc chuyển động theo phương trình: s = s(1). Suy ra s' (t) = v(t), do đó s(t) là một nguyên hàm của v(t). Ta có: \[\int {v\left( t \right)dt} = \int {4cost{\rm{dt}}} = 4sint + C.\]
Suy ra s(t)=4sint+C.
Tại thời điểm t = 0, ta có s(0) = 0, tức là 4sin0 + C = 0, hay C = 0. Vậy phương trình chuyển động của con lắc là: s(t) = 4sint.
Lời giải
a) Ta đã biết, công thức tính quãng đường s(t) xe ô tô đi được trong t (giây) là một nguyên hàm của hàm v(t). Do \[\int {\left( { - 10t + 30} \right)dt} {\rm{ }} = - 5{t^2} + 30t + C\]
nên ta có: \[s(t) = - 5{t^2} + 30t + C\] với C là hằng số. Do s(0) = 0 nên C = 0. Suy ra \[s(t) = - 5{t^2} + 30t\].
b) Xe ô tô dừng hẳn khi v(t) = 0, tức là – 10t + 30 = 0 hay t= 3.
Vậy thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là 3 giây.
c) Ta có: tốc độ 72 km/h cũng là tốc độ 20 m/s.
Do đó, quãng đường xe ô tô còn di chuyển được kể từ lúc đạp phanh đến khi xe dừng hẳn là:
s(3) = − 5 .32 + 30 . 3 = 45 (m).
Vậy quãng đường xe ô tô đã di chuyển kể từ lúc người lái xe phát hiện chướng ngại vật trên đường đến khi xe ô tô dừng hẳn là: 20 +45 = 65 (m).
Do 65 < 80 nên xe ô tô đã dừng hẳn trước khi va chạm với chướng ngại vật trên đường. Vì thế, tai nạn đã không xảy ra đối với xe ô tô đó.Lời giải
|
Vì a(t) = v’(t) nên: \[v(t) = \int {a(t)dt} = \int {10dt = 10t + C} \]. |
||
|
Ta có: v(0) = 0 nên 10.0 + C = 0 hay C = 0. Vậy v(t) = 10t (m/s) |
||
|
Vì v(t) = s’(t) nên: \[s(t) = \int {v(t)dt} = \int {10tdt = 5{t^2} + C} \]. |
||
|
Ta có: s(0) = 0 nên 5.02 + C = 0 hay C = 0. Vậy s(t) = 5t2 (m)
|
Lời giải
Gọi \({\rm{S}} = {\rm{S}}({\rm{t}})\) là quãng đường rơi được của hòn đá tại thời điểm \({\rm{t}}({\rm{S}}({\rm{t}})\) tính theo m , t tính theo giây).
Suy ra \({S^\prime }({\rm{t}}) = {\rm{v}}({\rm{t}})\), do đó \({\rm{S}}({\rm{t}})\) là một nguyên hàm của \(v({\rm{t}})\).
Ta có \(\int v (t)dt = \int 9 ,8tdt = 4,9{t^2} + C\). Suy ra \({\rm{S}}({\rm{t}}) = 4,9{{\rm{t}}^2} + {\rm{C}}\).
Mà hòn đá rơi từ mỏm đá có độ cao 150 m so với mặt đất theo phương thẳng đứng tức là tại thời điểm \({\rm{t}} = 0\) thì \({\rm{S}} = 0\) hay \({\rm{S}}(0) = 0\), suy ra \({\rm{C}} = 0\).
Vậy công thức tính quãng đường rơi được \({\rm{S}}({\rm{t}})\) của hòn đá tại thời điểm t là: \(S(t) = 4,9{t^2}.\)
Khi hòn đá chạm đất thì \({\rm{S}}({\rm{t}}) = 150\). Ta có \(4,9{{\rm{t}}^2} = 150\). Suy ra \(t = \pm \frac{{10\sqrt {15} }}{7}\).
Mà \({\rm{t}} > 0\) nên \(t = \frac{{10\sqrt {15} }}{7}\). Vậy sau \(t = \frac{{10\sqrt {15} }}{7} \approx 5,53\) giây thì hòn đá chạm đến mặt đất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.