15 bài tập Một số bài toán liên quan thực tế (có lời giải)

Vì \((Q)//(P)\) nên \((Q)\) có vecơo pháp tuyến là \(\vec n = (6;5;1)\).

Phương trình mặt phẳng \((Q)\) là: \(6(x - 1) + 5(y - 1) + 1(z - 1) = 0 \Leftrightarrow 6x + 5y + z - 12 = 0.\)

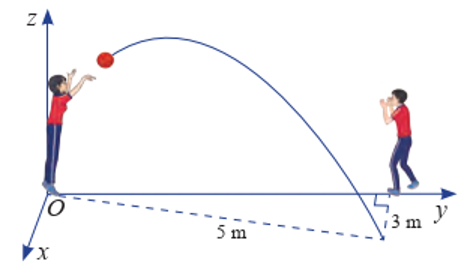
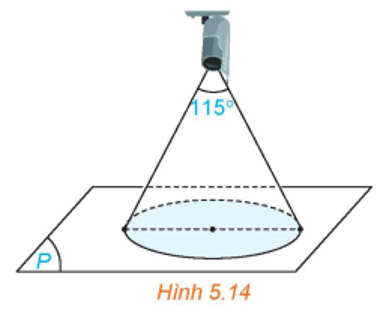
Gọi \(M\) là điểm mà quả bóng rơi trên mặt đất.

Khi đó \(M(3;4;0)\). Mặt phẳng \((P)\) có cặp vectơ chỉ phương là \(\vec k = (0;0;1)\) và \(\overrightarrow {OM}  = (3;4;0)\) nên mặt phẳng \((P)\) có vectơ pháp tuyến là \(\vec n = ( - 4;3;0)\).

Phương trình mặt phẳng \((P)\) là \( - 4x + 3y = 0\).

\((P)//(Q);(P)\) vuông góc với \((R);(Q)\) vuông góc với \((R)\).

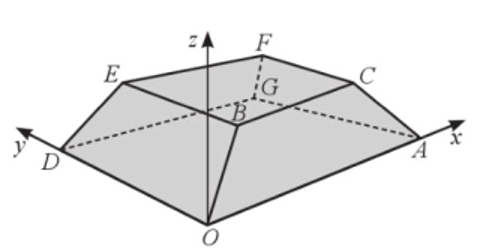
a) Phương trình mặt phẳng \((ABC)\) là: \(\frac{x}{3} + \frac{y}{3} + \frac{z}{2} = 1{\rm{   }}(*)\)

b) Thay toạ độ của điểm \(D\) vào vế trái của phương trình (*), ta có: \(\frac{1}{3} + \frac{1}{3} + \frac{1}{2} \ne 1\). Suy ra điểm \(D\) không thuộc mặt phẳng \((ABC)\).

Vậy bốn điểm A, B, C, D không đồng phẳng.

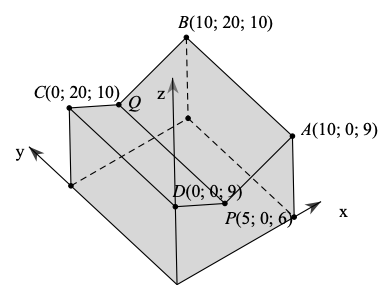
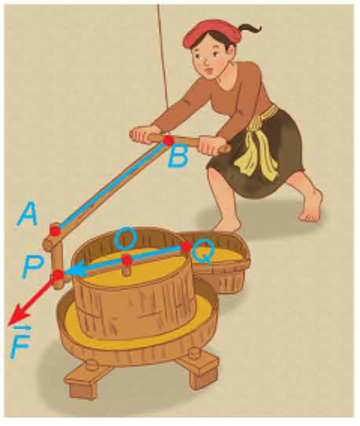
a) Hai mặt phẳng tương ứng mỗi mái nhà là \((ABP)\) và \((CDP)\).

\( \bullet \) Do mặt phẳng \((ABP)\) có cặp vectơ chỉphương là \(\overrightarrow {AB}  = (0;20;1),\overrightarrow {AP}  = ( - 5;0; - 3)\) nên có một vectơ pháp tuyến là: \([\overrightarrow {AB} ,\overrightarrow {AP} ] = \left( {\left| {\begin{array}{*{20}{c}}{20}&1\\0&{ - 3}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&0\\{ - 3}&{ - 5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{20}\\{ - 5}&0\end{array}} \right|} \right) = ( - 60; - 5;100).\)

Mà mặt phẳng \((ABP)\) đi qua điểm \(A(10;0;9)\) nên có phương trình là:

\( - 60(x - 10) - 5(y - 0) + 100(z - 9) = 0 \Leftrightarrow 12x + y - 20z + 60 = 0.\)

\( \bullet \) Do mặt phẳng \((CDP)\) có cặp vectơ chỉ phương là \(\overrightarrow {DP}  = (5;0; - 3),\overrightarrow {DC}  = (0;20;1)\) nên có một vectơ pháp tuyến là: \([\overrightarrow {DP} ,\overrightarrow {DC} ] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - 3}\\{20}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 3}&5\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}5&0\\0&{20}\end{array}} \right|} \right) = (60; - 5;100).\)

Mà mặt phẳng \((CDP)\) đi qua điểm \(D(0;0;9)\) nên có phương trình là:

\(60(x - 0) - 5(y - 0) + 100(z - 9) = 0 \Leftrightarrow 12x - y + 20z - 180 = 0.\)

b) Vì các bức tường của nhà kho đều được xây vuông góc với mặt đất nên vởi hệ toạ độ trên ta có \(Q(x;20;z)\).

Do điểm \(Q\) thuộc mặt phẳng \((ABP)\) nên toạ độ của điểm \(Q\) thoả mãn:

\(12x + 20 - 20z + 60 = 0,{\rm{ t?c l\`a  }}3x - 5z =  - 20.{\rm{ }}\)

Do điểm \(Q\) thuộc mặt phẳng \((CDP)\) nên toạ độ của điểm \(Q\) thoả mãn \(12x - 20 + 20z - 180 = 0\), tức là \(3x + 5z = 50\).

Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{3x - 5z =  - 20}\\{3x + 5z = 50}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 5}\\{z = 7}\end{array}} \right.} \right.\). Vậy \(Q(5;20;7)\).

c) Với \(P(5;0;6)\) và \(Q(5;20;7)\) ta có: \(\overrightarrow {PQ}  = (0;20;1)\).