Trong không gian với hệ tọa độ Oxyz ( đơn vị trên trục tọa độ là kiloomet), một máy bay đang ở vị trí A(3; -2,5; 0,5) và sẽ hạ cánh ở vị trí B(3; 7,5; 0) trên đường băng như hình bên dưới

a) Sau bao nhiêu phút máy bay từ vị trí A hạ cánh tại vị trí B? Biết tọa độ của máy bay là 300 km/h trên quãng đường AB (làm tròn kết quả đến hàng đơn vị của phút)

b) Có một lớp mây được mô phỏng bởi một mặt phẳng \[\left( \alpha  \right)\] đi qua ba điểm \[M(9;0;0)\], \[N(0; - 9;0)\], \[P(0;0;0,9)\]. Tính độ cao của máy bay khi máy bay xuyên qua đám mây để hạ cánh.

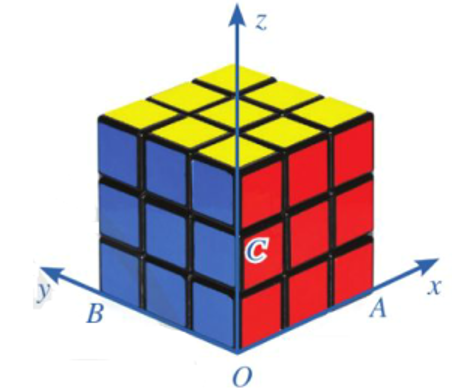
a) Vì \(B(4k;3k;2k)\) thuộc mặt phẳng \((CBEF):z = 3\) nên \(2k = 3\), suy ra \(k = \frac{3}{2}\). Vậy \(B\left( {6;\frac{9}{2};3} \right)\).

b) Ta có: \(\overrightarrow {OA}  = (50;0;0),\overrightarrow {OB}  = \left( {6;\frac{9}{2};3} \right)\) nên \([\overrightarrow {OA} ,\overrightarrow {OB} ] = \left( {\left| {\begin{array}{*{20}{c}}0&0\\{\frac{9}{2}}&3\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{50}\\3&6\end{array}} \right|;{\mkern 1mu} \left| {\begin{array}{*{20}{c}}{50}&0\\6&{\frac{9}{2}}\end{array}} \right|} \right) = (0; - 150;225).\)

Suy ra \(\vec n = (0; - 2;3)\) là một vectơ pháp tuyến của mặt phẳng \((AOBC)\).

Vậy phương trình mặt phẳng \((AOBC)\) là: \(0 \cdot (x - 0) + ( - 2) \cdot (y - 0) + 3 \cdot (z - 0) = 0 \Leftrightarrow 2y - 3z = 0.\)

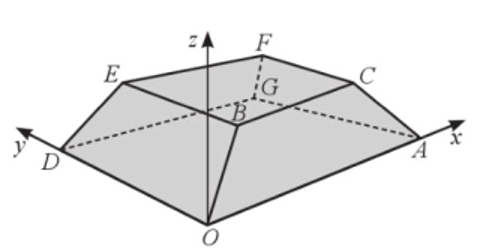
c) Ta có:\(\overrightarrow {OD}  = (0;20;0),\overrightarrow {OB}  = \left( {6;\frac{9}{2};3} \right)\) nên \([\overrightarrow {OD} ,\overrightarrow {OB} ] = \left( {\left| {\begin{array}{*{20}{c}}{20}&0\\{\frac{9}{2}}&3\end{array}} \right|;\left| {\begin{array}{*{20}{l}}0&0\\3&6\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{20}\\6&{\frac{9}{2}}\end{array}} \right|} \right) = (60;0; - 120){\rm{. }}\)

Suy ra \(\vec u = (1;0; - 2)\) là một vectơ pháp tuyến của mặt phẳng \((DOBE)\).

Vậy phương trình mặt phẳng \((DOBE)\) là: \(1 \cdot (x - 0) + 0 \cdot (y - 0) + ( - 2) \cdot (z - 0) = 0 \Leftrightarrow x - 2z = 0.\)

d) Một vec tơ pháp tuyến của mặt phẳng \((AOBC)\) và \((DOBE)\) lần lượt là: \(\vec p = (0;2; - 3)\) và \(\vec q = ( - 1;0;2)\).

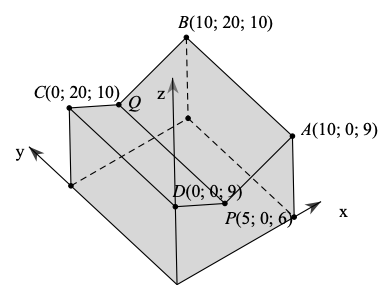
a) Ta có:\(\overrightarrow {AB}  = (2;2;0),\overrightarrow {AC}  = (4;2; - 0,5)\) nên \([\overrightarrow {AB} ,\overrightarrow {AC} ] = \left( {\left| {\begin{array}{*{20}{c}}2&0\\2&{ - 0,5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&2\\{ - 0,5}&4\end{array}} \right|;\left| {\begin{array}{*{20}{l}}2&2\\4&2\end{array}} \right|} \right) = ( - 1;1; - 4)\)

là một vectơ pháp tuyến của mặt phẳng \((ABC)\).

Vậy phương trình mặt phẳng \((ABC)\) là: \(( - 1) \cdot (x - 2) + 1 \cdot (y - 1) + ( - 4) \cdot (z - 3) = 0 \Leftrightarrow x - y + 4z - 13 = 0.{\rm{ }}\)

b) Vì\(4 - 0 + 4 \cdot 2,8 - 13 = 2,2 \ne 0\) nên điểm \(D(4;0;2,8)\) không thuộc mặt phẳng \((ABC)\). Vậy bốn điểm A, B, C, D không đồng phẳng.