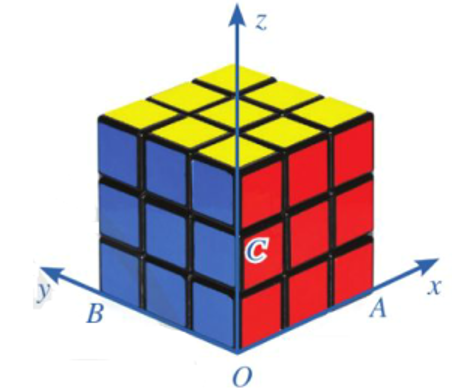
Khối rubik được gắn vơi hệ toạ độ Oxyz có đơn vị bằng độ dài cạnh hình lập phương nhỏ (Hình vẽ ). Xét bốn điểm \(A(3;0;0),B(0;3;0),C(0;0;2)\) và \(D(1;1;1)\).
a) Lập phương trình mặt phẳng đi qua ba điểm A, B, C.
b) Bốn điểm A, B, C, D có đồng phẳng hay không?
Khối rubik được gắn vơi hệ toạ độ Oxyz có đơn vị bằng độ dài cạnh hình lập phương nhỏ (Hình vẽ ). Xét bốn điểm \(A(3;0;0),B(0;3;0),C(0;0;2)\) và \(D(1;1;1)\).
a) Lập phương trình mặt phẳng đi qua ba điểm A, B, C.
b) Bốn điểm A, B, C, D có đồng phẳng hay không?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Phương trình mặt phẳng \((ABC)\) là: \(\frac{x}{3} + \frac{y}{3} + \frac{z}{2} = 1{\rm{ }}(*)\)
b) Thay toạ độ của điểm \(D\) vào vế trái của phương trình (*), ta có: \(\frac{1}{3} + \frac{1}{3} + \frac{1}{2} \ne 1\). Suy ra điểm \(D\) không thuộc mặt phẳng \((ABC)\).
Vậy bốn điểm A, B, C, D không đồng phẳng.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
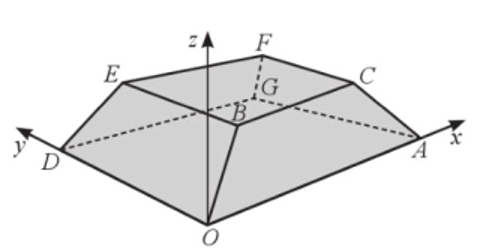
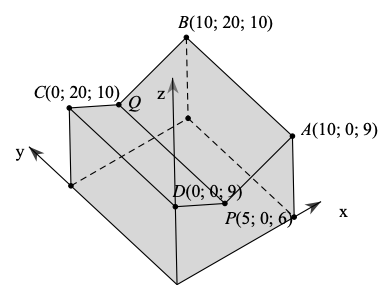
a) Vì \(B(4k;3k;2k)\) thuộc mặt phẳng \((CBEF):z = 3\) nên \(2k = 3\), suy ra \(k = \frac{3}{2}\). Vậy \(B\left( {6;\frac{9}{2};3} \right)\).
b) Ta có: \(\overrightarrow {OA} = (50;0;0),\overrightarrow {OB} = \left( {6;\frac{9}{2};3} \right)\) nên \([\overrightarrow {OA} ,\overrightarrow {OB} ] = \left( {\left| {\begin{array}{*{20}{c}}0&0\\{\frac{9}{2}}&3\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{50}\\3&6\end{array}} \right|;{\mkern 1mu} \left| {\begin{array}{*{20}{c}}{50}&0\\6&{\frac{9}{2}}\end{array}} \right|} \right) = (0; - 150;225).\)
Suy ra \(\vec n = (0; - 2;3)\) là một vectơ pháp tuyến của mặt phẳng \((AOBC)\).
Vậy phương trình mặt phẳng \((AOBC)\) là: \(0 \cdot (x - 0) + ( - 2) \cdot (y - 0) + 3 \cdot (z - 0) = 0 \Leftrightarrow 2y - 3z = 0.\)
c) Ta có:\(\overrightarrow {OD} = (0;20;0),\overrightarrow {OB} = \left( {6;\frac{9}{2};3} \right)\) nên \([\overrightarrow {OD} ,\overrightarrow {OB} ] = \left( {\left| {\begin{array}{*{20}{c}}{20}&0\\{\frac{9}{2}}&3\end{array}} \right|;\left| {\begin{array}{*{20}{l}}0&0\\3&6\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{20}\\6&{\frac{9}{2}}\end{array}} \right|} \right) = (60;0; - 120){\rm{. }}\)
Suy ra \(\vec u = (1;0; - 2)\) là một vectơ pháp tuyến của mặt phẳng \((DOBE)\).
Vậy phương trình mặt phẳng \((DOBE)\) là: \(1 \cdot (x - 0) + 0 \cdot (y - 0) + ( - 2) \cdot (z - 0) = 0 \Leftrightarrow x - 2z = 0.\)
d) Một vec tơ pháp tuyến của mặt phẳng \((AOBC)\) và \((DOBE)\) lần lượt là: \(\vec p = (0;2; - 3)\) và \(\vec q = ( - 1;0;2)\).
Lời giải
a) Ta có:\(\overrightarrow {AB} = (2;2;0),\overrightarrow {AC} = (4;2; - 0,5)\) nên \([\overrightarrow {AB} ,\overrightarrow {AC} ] = \left( {\left| {\begin{array}{*{20}{c}}2&0\\2&{ - 0,5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&2\\{ - 0,5}&4\end{array}} \right|;\left| {\begin{array}{*{20}{l}}2&2\\4&2\end{array}} \right|} \right) = ( - 1;1; - 4)\)
là một vectơ pháp tuyến của mặt phẳng \((ABC)\).
Vậy phương trình mặt phẳng \((ABC)\) là: \(( - 1) \cdot (x - 2) + 1 \cdot (y - 1) + ( - 4) \cdot (z - 3) = 0 \Leftrightarrow x - y + 4z - 13 = 0.{\rm{ }}\)
b) Vì\(4 - 0 + 4 \cdot 2,8 - 13 = 2,2 \ne 0\) nên điểm \(D(4;0;2,8)\) không thuộc mặt phẳng \((ABC)\). Vậy bốn điểm A, B, C, D không đồng phẳng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo