Trong không gian Oxyz, một ngôi nhà có sàn nhà thuộc mặt phẳng Oxy , trần nhà tầng 1 thuộc mặt phẳng \(z - 1 = 0\), mái nhà tầng 2 thuộc mặt phẳng \(x + y + 50z - 100 = 0\). Hỏi trong ba mặt phẳng tương ứng chứa sàn nhà, trần tầng 1 , mái tầng 2 , hai mặt phẳng nào song song với nhau.
Trong không gian Oxyz, một ngôi nhà có sàn nhà thuộc mặt phẳng Oxy , trần nhà tầng 1 thuộc mặt phẳng \(z - 1 = 0\), mái nhà tầng 2 thuộc mặt phẳng \(x + y + 50z - 100 = 0\). Hỏi trong ba mặt phẳng tương ứng chứa sàn nhà, trần tầng 1 , mái tầng 2 , hai mặt phẳng nào song song với nhau.
Câu hỏi trong đề: 15 bài tập Một số bài toán liên quan thực tế (có lời giải) !!
Quảng cáo
Trả lời:
Vi mặt phẳng Oxy vuông góc với Oz nên mặt phẳng Oxy nhận \(\vec k = (0;0;1)\) làm một vectơ pháp tuyến.
Vi mặt phẳng Oxy đi qua điểm \({\rm{O}}(0;0;0)\) và có vectơ pháp tuyến \(\vec k = (0;0;1)\) nên có phương trình là: \(z - 0 = 0\) hay \(z = 0\).
Mặt phẳng \(z - 1 = 0\) có \(\overrightarrow {{n_1}} = (0;0;1)\)
vi \(\overrightarrow {{n_1}} = \vec k\) và \(0 \ne - 1\) nên mặt phẳng chứa sàn nhà song song với trần tầng 1 .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
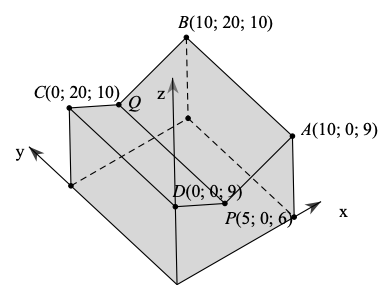
a) Vì \(B(4k;3k;2k)\) thuộc mặt phẳng \((CBEF):z = 3\) nên \(2k = 3\), suy ra \(k = \frac{3}{2}\). Vậy \(B\left( {6;\frac{9}{2};3} \right)\).
b) Ta có: \(\overrightarrow {OA} = (50;0;0),\overrightarrow {OB} = \left( {6;\frac{9}{2};3} \right)\) nên \([\overrightarrow {OA} ,\overrightarrow {OB} ] = \left( {\left| {\begin{array}{*{20}{c}}0&0\\{\frac{9}{2}}&3\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{50}\\3&6\end{array}} \right|;{\mkern 1mu} \left| {\begin{array}{*{20}{c}}{50}&0\\6&{\frac{9}{2}}\end{array}} \right|} \right) = (0; - 150;225).\)
Suy ra \(\vec n = (0; - 2;3)\) là một vectơ pháp tuyến của mặt phẳng \((AOBC)\).
Vậy phương trình mặt phẳng \((AOBC)\) là: \(0 \cdot (x - 0) + ( - 2) \cdot (y - 0) + 3 \cdot (z - 0) = 0 \Leftrightarrow 2y - 3z = 0.\)
c) Ta có:\(\overrightarrow {OD} = (0;20;0),\overrightarrow {OB} = \left( {6;\frac{9}{2};3} \right)\) nên \([\overrightarrow {OD} ,\overrightarrow {OB} ] = \left( {\left| {\begin{array}{*{20}{c}}{20}&0\\{\frac{9}{2}}&3\end{array}} \right|;\left| {\begin{array}{*{20}{l}}0&0\\3&6\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{20}\\6&{\frac{9}{2}}\end{array}} \right|} \right) = (60;0; - 120){\rm{. }}\)
Suy ra \(\vec u = (1;0; - 2)\) là một vectơ pháp tuyến của mặt phẳng \((DOBE)\).
Vậy phương trình mặt phẳng \((DOBE)\) là: \(1 \cdot (x - 0) + 0 \cdot (y - 0) + ( - 2) \cdot (z - 0) = 0 \Leftrightarrow x - 2z = 0.\)
d) Một vec tơ pháp tuyến của mặt phẳng \((AOBC)\) và \((DOBE)\) lần lượt là: \(\vec p = (0;2; - 3)\) và \(\vec q = ( - 1;0;2)\).
Lời giải
a) Ta có:\(\overrightarrow {AB} = (2;2;0),\overrightarrow {AC} = (4;2; - 0,5)\) nên \([\overrightarrow {AB} ,\overrightarrow {AC} ] = \left( {\left| {\begin{array}{*{20}{c}}2&0\\2&{ - 0,5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&2\\{ - 0,5}&4\end{array}} \right|;\left| {\begin{array}{*{20}{l}}2&2\\4&2\end{array}} \right|} \right) = ( - 1;1; - 4)\)
là một vectơ pháp tuyến của mặt phẳng \((ABC)\).
Vậy phương trình mặt phẳng \((ABC)\) là: \(( - 1) \cdot (x - 2) + 1 \cdot (y - 1) + ( - 4) \cdot (z - 3) = 0 \Leftrightarrow x - y + 4z - 13 = 0.{\rm{ }}\)
b) Vì\(4 - 0 + 4 \cdot 2,8 - 13 = 2,2 \ne 0\) nên điểm \(D(4;0;2,8)\) không thuộc mặt phẳng \((ABC)\). Vậy bốn điểm A, B, C, D không đồng phẳng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.