20 câu Trắc nghiệm Toán 12 Chân trời sáng tạo Bài 1. Tính đơn điệu và cực trị của hàm số có đáp án
45 người thi tuần này 4.6 2 K lượt thi 20 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
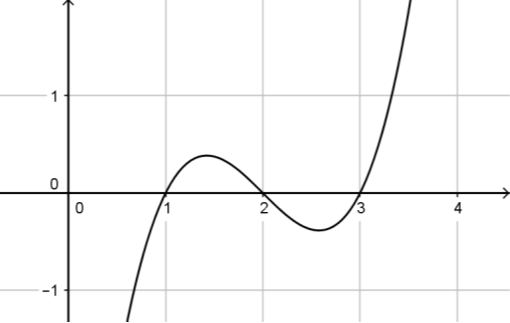
Câu 1
A. \(\left( { - 2\,;2} \right)\).
B. \(\left( {0\,;\,2} \right)\).
C. \(\left( { - 1\,;\,1} \right)\).
D. \(\left( {1\,;\,2} \right)\).
Lời giải
Đáp án đúng là: D
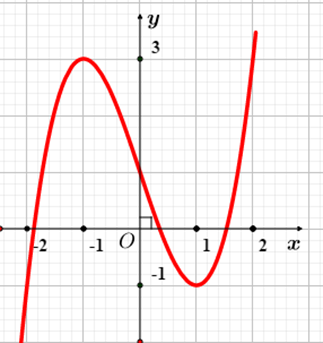
- Xét đáp án A, trên khoảng \(\left( { - 2\,;2} \right)\) đồ thị có đoạn hướng đi lên là hàm số đồng biến và có đoạn hướng đi xuống là hàm số nghịch biến nên loại.
- Xét đáp án B, trên khoảng \(\left( {0\,;\,2} \right)\) đồ thị có đoạn hướng đi xuống là hàm số nghịch biến và có đoạn hướng đi lên là hàm số đồng biến nên loại.
- Xét đáp án C, trên khoảng \(\left( { - 1\,;\,1} \right)\) đồ thị có hướng đi xuống là hàm số nghịch biến nên loại.
- Xét đáp án D, trên khoảng \(\left( {1\,;\,2} \right)\) đồ thị có hướng đi lên là hàm số đồng biến nên chọn.
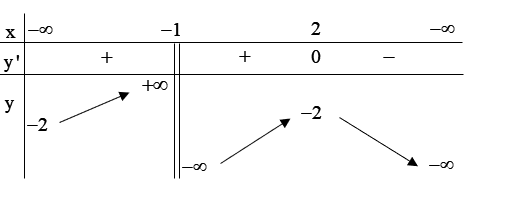
Câu 2
A. (0; 1).
B. (−∞; 1).
C. (−1; 1).
D. (−1; 0).
Lời giải
Đáp án đúng là: D
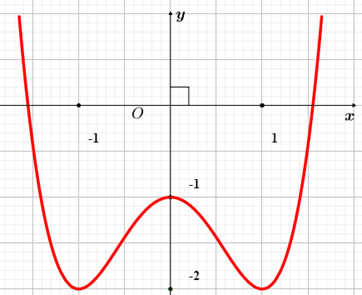
Quan sát đồ thị ta thấy đồ thị đi lên trong các khoảng \(( - 1;0)\) và \((1; + \infty ).\)
Vậy hàm số đồng biến trên các khoảng \(( - 1;0)\) và \((1; + \infty ).\)
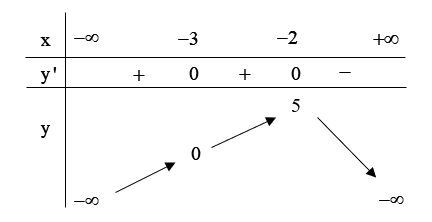
Câu 3
A. Hàm số đồng biến trên khoảng \(\left( { - 1;\,3} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( { - \infty ;\,2} \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( { - 2;\,1} \right)\).
D. Hàm số nghịch biến trên khoảng \(\left( {1;\,2} \right)\).
Lời giải
Đáp án đúng là: D
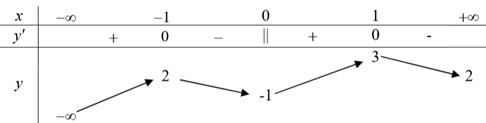
Dựa vào bảng biến thiên ta có hàm số nghịch biến trên khoảng \(\left( {1\,;\,2} \right)\).
Câu 4
A. \(x = - 3\).
B. \(x = 1\).
C. \(x = 0\).
D. \(x = 2\).
Lời giải
Đáp án đúng là: C
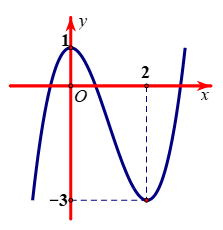
Từ đồ thị hàm số ta có hàm số đạt cực đại tại \(x = 0\).
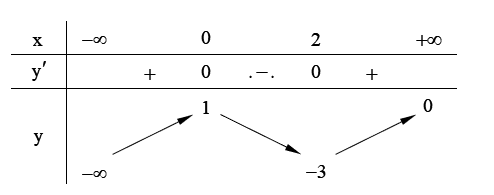
Câu 5
A. \[x = 0\].
B. \[x = 2\].
C. \[y = - 3\].
D. \[y = 1\].
Lời giải
Đáp án đúng là: D
Dựa vào bảng biến thiên ta có hàm số đạt cực đại tại \[x = 0\]và giá trị cực đại là \[y = 1\].
Câu 6
A. Hàm số nghịch biến trên khoảng \[\left( { - 3;1} \right)\].
B. Hàm số đồng biến trên \[\left( { - 9; - 5} \right)\].
C. Hàm số đồng biến trên \[\mathbb{R}\] .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Hàm số nghịch biến trên từng khoảng xác định của nó.
B. Hàm số đồng biến trên tập xác định của nó.
C. Hàm số đồng biến trên từng khoảng xác định của nó.
D. Hàm số nghịch biến trên tập xác định của nó.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \[(0;2).\]
B. \[(0; + \infty ).\]
C. \[( - \infty ;2).\]
D. \[( - \infty ;0)\] và \[(2; + \infty ).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. Hàm số đã cho đồng biến trên khoảng \[\left( { - \infty ;0} \right)\].
B. Hàm số đã cho đồng biến trên khoảng \[\left( {2; + \infty } \right)\].
C. Hàm số đã cho đồng biến trên khoảng \[\left( {0;2} \right)\].
D. Hàm số đã cho đồng biến trên khoảng \[\left( { - \infty ;3} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \[y = {x^3} - 3{x^2}\].
B. \[y = - {x^3} + 3{x^2} - 3x + 2\].
C. \[y = - {x^3} + 3x + 1\].
D. \[y = {x^3}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \(3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. 1.
B. 0.
C. 2.
D. 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. \(x = - 1.\)
B. \(x = 1.\)
C. \(x = - 3.\)
D. \(x = 3.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. Hàm số đã cho đồng biến trên các khoảng \(\left( { - 2; + \infty } \right)\) và \(\left( { - \infty ; - 2} \right).\)
B. Hàm số đã cho đồng biến trên \(\left( { - \infty ; - 1} \right) \cup \left( { - 1;2} \right).\)
C. Hàm số đã cho đồng biến trên khoảng \(\left( {0;2} \right).\)
D. Hàm số đã cho đồng biến trên \(\left( { - 2;2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. Đồ thị hàm số \(y = f(x)\) cắt trục hoành tại ba điểm phân biệt.
B. Đồ thị hàm số \(y = f(x)\) có hai điểm cực trị.
C. Đồ thị hàm số \(y = f(x)\) có ba điểm cực trị.
D. Đồ thị hàm số \(y = f(x)\) có một điểm có một điểm cực trị.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. \[5.\]
B. \[ - 5.\]
C. \[ - 4.\]
D. \[4.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. \[ - 8\].
B. \[ - 2\].
C. \[2\].
D. 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. (0; +∞).
B. (0; 3).
C. (−4; +∞).
D. (3; +∞).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. (0; 15).
B. (0; 10).
C. (15 ;25).
D. (10 ; 25).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.