32 bài tập Vận dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn (có lời giải)
37 người thi tuần này 4.6 695 lượt thi 32 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm và tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Tự luận
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Phương trình mặt phẳng
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 4. Ứng dụng hình học của tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 3. Tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Nguyên hàm của một số hàm số sơ cấp
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Nguyên hàm
Đề cương ôn tập giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Tự luận
Danh sách câu hỏi:
Lời giải
|
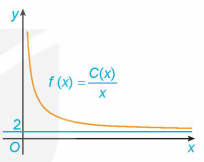
a) Khảo sát và vẽ đồ thị của hàm số C (v): |
|
Tập xác định: D = (0; 120]. |
|
Sự biến thiên: |
|
+ Chiều biến thiên: |
|
· Đạo hàm C '(v) = 0 ⇔ v = –80 (loại) hoặc v = 80. |
|
· Trên khoảng (0; 80), C '(v) < 0 nên hàm số nghịch biến trên khoảng này. |
|
· Trên khoảng (80; 120), C '(v) > 0 nên hàm số đồng biến trên khoảng này. |
|
+ Cực trị: Hàm số đạt cực tiểu tại v = 80, CCT = C(80) = 400. |
|
+ Giới hạn vô cực và tiệm cận: \[\mathop {\lim }\limits_{v \to {0^ + }} C(v) = + \infty \] nên đường thẳng v = 0 là tiệm cận đứng của đồ thị hàm số. |
|
+ Bảng biến thiên: 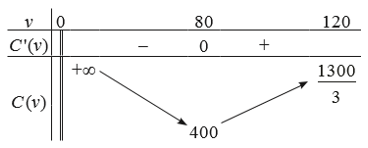 – Đồ thị:
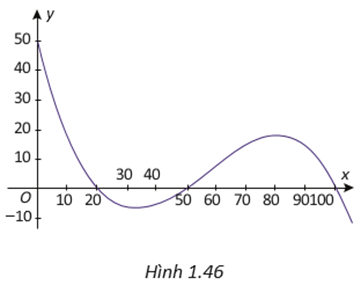
Đồ thị hàm số có điểm cực tiểu (80; 400) và đi qua các điểm (40; 500), (100; 410), (120; \[\frac{{1300}}{3}\]) như Hình vẽ bên dưới.
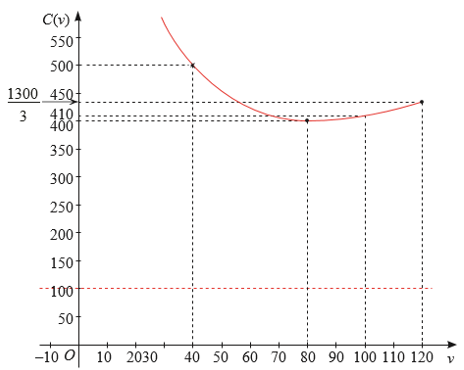 b) Quan sát đồ thị hàm số, ta nhận thấy hàm số đạt GTNN khi v = 80 và GTNN là 400. Như vậy, để tiết kiệm tiền xăng nhất, tài xế nên chạy xe với tốc độ trung bình là 80 km/h.
|
Lời giải
Đạo hàm L '(x) = –3x2 + 6x + 240; L '(x) = 0 ⇔ x = 10 hoặc x = –8 (loại).
Lời giải
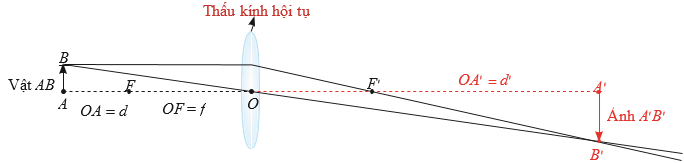
a) Vì \(d > 0\) nên với \(x = d\) thì \(x > 0\).
Xét hàm số \(y = \frac{{3x}}{{x - 3}}\) với \(x > 0\) và \(x \ne 3\).
Tập xác định: \(D = (0;3) \cup (3; + \infty )\).
Sự biến thiền:
Chiều biến thiên:
Đạo hàm \({y^\prime } = \frac{{ - 9}}{{{{(x - 3)}^2}}}\). Vi \({y^\prime } < 0\) với mọi \(x > 0\) và \(x \ne 3\) nên hàm số nghịch biến trên mỗi khoảng \((0;3)\) và \((3; + \infty )\).
Tiệm cận:
Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{3x}}{{x - 3}} = 3\). Suy ra đường thắng \(y = 3\) là tiệm cận ngang của đồ thị hàm số. Ta có \(\mathop {\lim }\limits_{x \to {3^ - }} y = \mathop {\lim }\limits_{x \to {3^3}} \frac{{3x}}{{x - 3}} = - \infty ;\mathop {\lim }\limits_{x \to {3^ + }} y = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{3x}}{{x - 3}} = + \infty \). Suy ra đường thẳng \({\rm{x}} = 3\) là tiệm cận đứng của đồ thị hàm số.
Bảng biến thiên:
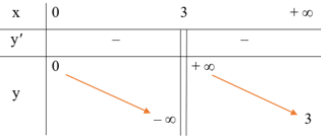
Đồ thị:
Đồ thị hàm số đi qua điếm \((2; - 6)\) và điếm \((6;6)\).
Đồ thị của hàm số đã cho được biếu diễn như hình dưới đây.
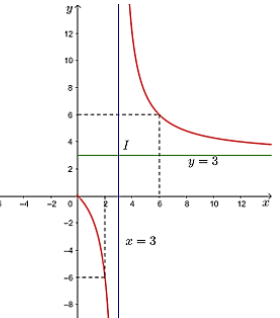
b) Đế vật là ảnh thật thì \({{\rm{d}}^\prime } > 0\), tức là \(y > 0\).
Quan sát đồ thị hàm số \(y = \frac{{3x}}{{x - 3}}\), ta thấy trên khoảng \((3; + \infty )\), đồ thị hàm số nằm phía trên trục \({\rm{Ox}}\) nên \({\rm{y}} > 0\) trên khoảng này. Vậy với \(x > 3\), tức \({\rm{d}} > 3\) hay khoảng cách từ vật đến thấy kính lớn hơn 3 thì ảnh của vật là ảnh thật.
Đế vật là ảnh áo thì \({{\rm{d}}^\prime } < 0\), tức là \(y < 0\).
Quan sát đồ thị hàm số \(y = \frac{{3x}}{{x - 3}}\), ta thấy trên khoáng \((0;3)\), đồ thị hàm số nằm phía dưới trục Ox nên \({\rm{y}} < 0\) trên khoảng này. Vậy với \(x \in (0;3)\), tức \(d \in (0;3)\) hay khoảng cách từ vật đến thấu kính lớn hơn 0 và nhỏ hơn 3 thì ảnh của vật là ảnh âo.
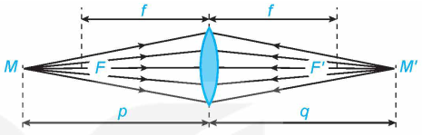
c) Khi vật tiến gần đến tiêu điếm, tức vị trí \(A\) tiến gần đến vị trí \(F\), thì khoáng cách $A F$ dần tiến tới 0 , hay \({\rm{d}} - {\rm{f}} \to 0\), suy ra \({\rm{d}} \to {\rm{f}}\), tức là \({\rm{x}} \to 3\).
Lời giải
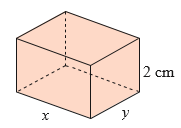
a) Thế tích của hình hộp chữ nhật cần chế tạo là: \(V = 2xy\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\).
Theo bài ra ta có \(V = 500\;{\rm{c}}{{\rm{m}}^3}\), khi đó \(2xy = 500\), suy ra \(y = \frac{{250}}{x}\).
b) Diện tích xung quanh của chiếc hộp là: \({{\rm{S}}_{{\rm{xq}}}} = 2({\rm{x}} + {\rm{y}}) \cdot 2 = 4({\rm{x}} + {\rm{y}})\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Diện tích toàn phần của chiếc hộp là: \({{\rm{S}}_{{\rm{tp}}}} = {{\rm{S}}_{{\rm{xq}}}} + 2\;{{\rm{S}}_{\rm{t}}} = 4({\rm{x}} + {\rm{y}}) + 2{\rm{xy}}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Lại có \({\rm{y}} = \frac{{250}}{x}\) nên \({{\rm{S}}_{{\rm{tp}}}} = 4\left( {x + \frac{{250}}{x}} \right) + 2x \cdot \frac{{250}}{x} = 4x + \frac{{1000}}{x} + 500\).
Vậy diện tích toàn phần của chiếc hộp là \(S(x) = 500 + 4x + \frac{{1000}}{x}\).
c) Xét hàm số \(S(x) = 500 + 4x + \frac{{1000}}{x}\) với \(x \in (0; + \infty )\).
Ta có \(S(x) = 4 - \frac{{1000}}{{{x^2}}}\);
Trên khoảng \((0; + \infty ),S(x) = 0\) khi \(x = 5\sqrt {10} \).
Ta có \(\mathop {\lim }\limits_{x \to {0^ - }} S(x) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {500 + 4x + \frac{{1000}}{x}} \right) = + \infty \);
\(\mathop {\lim }\limits_{x \to + \infty } S(x) = \mathop {\lim }\limits_{x \to + \infty } \left( {500 + 4x + \frac{{1000}}{x}} \right) = + \infty \)
Bảng biến thiên
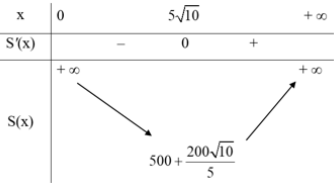
d) Đế dùng ít vật liệu nhất thì diện tích toàn phần của chiếc hộp phải nhó nhất.
Căn cứ vào bảng biến thiên ở câu c), ta thấy hàm số \(S({\rm{X}})\) đạt giá trị nhó nhất bằng: \(500 + \frac{{200\sqrt {10} }}{5}\)
tại \(x = 5\sqrt {10} \). Với \(x = 5\sqrt {10} \), ta có \(y = \frac{{250}}{{5\sqrt {10} }} = 5\sqrt {10} \).
Vậy kích thước 3 cạnh của chiếc hộp là \(2\;{\rm{cm}},5\sqrt {10} \;{\rm{cm}},5\sqrt {10} \;{\rm{cm}}\) thì dùng ít vật liệu nhất.
Lời giải
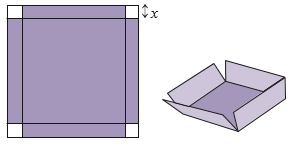
a) Sau khi cắt bốn góc tấm bìa và dựng thành chiếc hộp không nắp, khi đó chiếc hộp dựng thành có dạng hình hộp chữ nhật với các kích thước là \({\rm{x}},6 - 2{\rm{x}}\) và \(6 - 2{\rm{x}}({\rm{dm}})\).
Rõ ràng \({\rm{x}}\) phải thỏa mãn điều kiện \(0 < {\rm{x}} < 3\).
Thể tích của chiếc hộp là \({\rm{V}}({\rm{x}}) = {\rm{x}}{(6 - 2{\rm{x}})^2}\left( {{\rm{d}}{{\rm{m}}^3}} \right)\quad (0 < {\rm{x}} < 3)\).
b) Xét hàm số \({\rm{V}}({\rm{x}}) = {\rm{x}}{(6 - 2{\rm{x}})^2}\) với \({\rm{x}} \in (0;3)\).
Tập xác định: \({\rm{D}} = (0;3)\).
Sự biến thiên:
Chiều biến thiên:
Đạo hàm \({{\rm{V}}^\prime }({\rm{x}}) = {(6 - 2{\rm{x}})^2} + {\rm{x}} \cdot 2(6 - 2{\rm{x}}) \cdot ( - 2) = (6 - 2{\rm{x}})(6 - 6{\rm{x}})\).
Trên khoảng \((0;3)\), ta có \({{\rm{V}}^\prime }({\rm{x}}) = 0 \Leftrightarrow {\rm{x}} = 1\).
Trên khoảng \((0;1),{{\rm{V}}^\prime }({\rm{x}}) > 0\) nên hàm số đồng biến trên khoảng đó.
Trên khoảng \((1;3),{{\rm{V}}^\prime }({\rm{x}}) < 0\) nên hàm số nghịch biến trên khoảng đó.
Hàm số có một điểm cực trị là điểm cực đại tại \({\rm{x}} = 1,{{\rm{y}}_{{\rm{CD}}}} = 16\).
Bảng biến thiên:
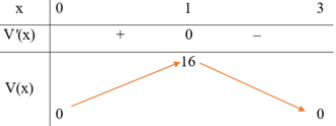
Đồ thị:
Trên khoảng \((0;3)\), đồ thị hàm số đi qua các điểm \((1;16)\) và \((2;8)\).
Đồ thị hàm số \({\rm{V}}({\rm{x}})\) trên khoảng \((0;3)\) được biểu diễn như hình dưới đây.
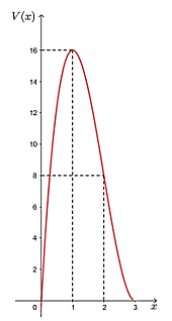
Từ đó, ta thấy đế tìm được độ dài cạnh hình vuông cần cắt bó để chiếc hộp đạt thế tích lớn nhất, ta cần tìm \({x_0} \in (0;3)\) sao cho \({\rm{V}}\left( {{{\rm{x}}_0}} \right)\) có giá trị lớn nhất.
Căn cứ vào bảng biến thiên ta thấy trong khoảng \((0;3)\) hàm số có một điếm cực trị duy nhất là điếm cực đại \(x = 1\) nên tại đó \({\rm{V}}({\rm{x}})\) có giá trị lớn nhất là \({\max _{(0;3)}}V(x) = 16\).
Vậy độ dài cạnh của hình vuông cần cắt bỏ là \(1{\rm{dm}}\) thì chiếc hộp có thế tích lớn nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.