Một cốc chứa 30 ml dung dịch KOH (potassium hydroxide) với nồng độ 100 mg/ml. Một bình chứa dung dịch KOH khác với nồng độ 8 mg/ml được trộn vào cốc.
a) Tính nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa, kí hiệu là C(x).
b) Coi C(x) là hàm số xác định với x ≥ 0. Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
c) Giải thích tại sao nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8 mg/ml.
Một cốc chứa 30 ml dung dịch KOH (potassium hydroxide) với nồng độ 100 mg/ml. Một bình chứa dung dịch KOH khác với nồng độ 8 mg/ml được trộn vào cốc.
a) Tính nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa, kí hiệu là C(x).
b) Coi C(x) là hàm số xác định với x ≥ 0. Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
c) Giải thích tại sao nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8 mg/ml.
Quảng cáo
Trả lời:
a) Tống khối lượng \({\rm{KOH}}\) sau khi trộn là: \(30.100 + 8.{\rm{x}} = 3000 + 8{\rm{x}}({\rm{mg}})\).
Tống thế tích dung dịch sau khi trộn là: \(30 + {\rm{x}}({\rm{ml}})\).
Nồng độ \({\rm{KOH}}\) trong cốc sau khi trộn là \(C(x) = \frac{{3000 + 8x}}{{30 + x}}({\rm{mg}}/{\rm{ml}})\).
b) \(C(x) = \frac{{3000 + 8x}}{{30 + x}},x \ge 0\)
Tập xác định của hàm số là \(D = [0; + \infty )\).
Sự biến thiên
Có \({C^\prime }(x) = \frac{{8(30 + x) - (3000 + 8x)}}{{{{(30 + x)}^2}}} = \frac{{ - 2760}}{{{{(30 + x)}^2}}} < 0\) với mọi \({x^3}0\).
Hàm số luôn nghịch biến trên \([0; + \infty )\).
Hàm số không có cực trị.
Tiệm cận
\(\mathop {\lim }\limits_{x \to + \infty } C(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{3000 + 8x}}{{30 + x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{3000}}{x} + 8}}{{\frac{{30}}{x} + 1}} = 8\)
Do đó \(y = 8\) là tiệm cận ngang của đồ thị hàm số (phần bên phải trục \({\rm{Oy}}\) ).
Bảng biến thiên
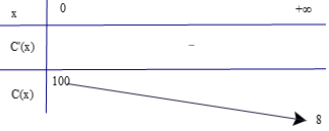
Đồ thị
Hàm số giao với trục \({\rm{Oy}}\) tại điểm \((0;100)\).
Hàm số đi qua điếm \(\left( {120;\frac{{132}}{5}} \right);(200;20)\).
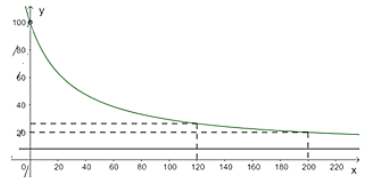
c) Vì \({C^\prime }(x) = \frac{{ - 2760}}{{{{(30 + x)}^2}}} < 0,\forall x \ge 0\) và \(\mathop {\lim }\limits_{x \to + \infty } C(x) = 8\) nên nồng độ \({\rm{KOH}}\) trong cốc giảm theo \(x\) nhưng luôn lớn hơn \(8{\rm{mg}}/{\rm{ml}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
2) Đồ thị
• Giao điểm của đồ thị với trục tung: (0:2).
• Đồ thị hàm số đi qua điểm (1 ; 6).
Vậy đồ thị hàm số \[y = f(t) = \frac{{26t + 10}}{{t + 5}},t \ge 0\] thể hiện như hình vẽ dưới đây: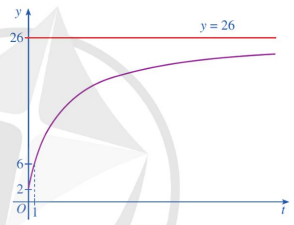
Lời giải
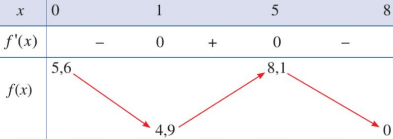
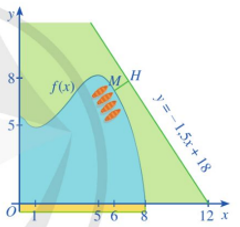
Căn cứ bảng biến thiên, ta có: \[\mathop {\max }\limits_{\left[ {0;8} \right]} \] f(x)= f(5)=8,1 tại x= 5.
c) Xét điểm M(x ; f(x)) thuộc đồ thị hàm số \[y = f(x) = \frac{1}{{10}}( - {x^3} + 9{x^2} - 15x + 56)\] với 0 ≤ x ≤8.
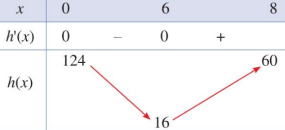
Căn cứ bảng biến thiên, ta có: h(x) > 0 với 0≤x≤8;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.