Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250 km so với bề mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao h của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm:
h(t) = -0,01t3 + 1,1t2 - 30t+250, trong đó t là thời gian tính bằng giây và h là độ cao tính bằng kilômét (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016).
a) Vẽ đồ thị của hàm số y= h(t) với 0≤ t ≤50 (đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 10 km).
b) Gọi v(t) là vận tốc tức thời của con tàu ở thời điểm t (giây) kể từ khi đốt cháy các tên lửa hãm với 0 ≤ t ≤50. Xác định hàm số v(t).
c) Vận tốc tức thời của con tàu lúc bắt đầu hãm phanh là bao nhiêu? Tại thời điểm t = 25 (giây) là bao nhiêu?
d) Tại thời điểm t = 25 (giây), vận tốc tức thời của con tàu vẫn giảm hay đang tăng trở lại?
e) Tìm thời điểm t (0 ≤ t ≤50) sao cho con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng. Khoảng cách nhỏ nhất này là bao nhiêu?
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250 km so với bề mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao h của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm:
h(t) = -0,01t3 + 1,1t2 - 30t+250, trong đó t là thời gian tính bằng giây và h là độ cao tính bằng kilômét (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016).
a) Vẽ đồ thị của hàm số y= h(t) với 0≤ t ≤50 (đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 10 km).
b) Gọi v(t) là vận tốc tức thời của con tàu ở thời điểm t (giây) kể từ khi đốt cháy các tên lửa hãm với 0 ≤ t ≤50. Xác định hàm số v(t).
c) Vận tốc tức thời của con tàu lúc bắt đầu hãm phanh là bao nhiêu? Tại thời điểm t = 25 (giây) là bao nhiêu?
d) Tại thời điểm t = 25 (giây), vận tốc tức thời của con tàu vẫn giảm hay đang tăng trở lại?
e) Tìm thời điểm t (0 ≤ t ≤50) sao cho con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng. Khoảng cách nhỏ nhất này là bao nhiêu?
Quảng cáo
Trả lời:
a) Xét hàm số \(h(t) = - 0,01{t^3} + 1,1{t^2} - 30t + 250\) với \(t \in [0;50]\).
Ta có \(h(t) = - 0,03{t^2} + 2,2t - 30\);
Trên khoảng \((0;50),h(t) = 0\) khi \(t \approx 18\).
\(h(0) = 250;h(18) = 8,08;h(50) = 250.{\rm{ }}\)
Do đó, \[\min h(t) = 8,08\] tại \({\rm{t}} = 18\) trên đoạn [0. 50]
Vậy tại thời điểm \(t = 18\) giây thì con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng và khoảng cách nhỏ nhất này bằng \(8,08\;{\rm{km}}\).
b) Xét hàm số \(h(t) = - 0,01{t^3} + 1,1{t^2} - 30t + 250\) với \(t \in [0;70]\).
Ta có \(h(t) = - 0,03{t^2} + 2,2t - 30\);
Trên khoảng \((0;70),h(t) = 0\) khi \(t \approx 18\) hoặc \(t \approx 55\).
Bảng biến thiên của hàm số \({\rm{h}}({\rm{t}})\) như sau:
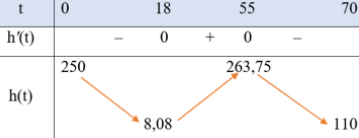
Trên khoảng \((0;70)\), đồ thị hàm số \({\rm{h}}({\rm{t}})\) đi qua các điểm \((0;250),(10;50),(50;250)\) và \((60;250)\).
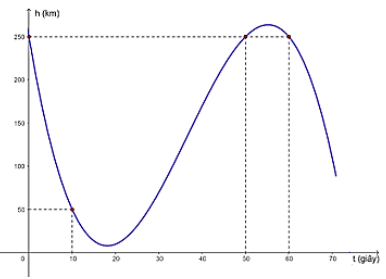
c) Ta có \({\rm{v}}({\rm{t}})\) là vận tốc tức thời của con tàu ở thời điểm \(t\) (giây) kế từ khi đốt cháy các tên lửa hām với \(0 \le t \le 50\).
Khi đó \({\rm{v}}({\rm{t}}) = {\rm{h}}({\rm{t}}) = - 0,03{{\rm{t}}^2} + 2,2{\rm{t}} - 30\) với \({\rm{t}} \in [0;50]\).
d) \(v(25) = - 0,03 \cdot {25^2} + 2,2 \cdot 25 - 30 = 6,25(\;{\rm{km}}/{\rm{s}})\).
e) Tại thời điếm \(t = 25\) (giây), lúc đó \(t \in (18;55)\), căn cứ vào bảng biến thiên ở câu \({\rm{b}}\) ), ta thấy rằng \(h({\rm{t}}) > 0\), tức là \(v(t) > 0\), vậy vận tốc tức thời của con tàu đang tăng trở lại.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
2) Đồ thị
• Giao điểm của đồ thị với trục tung: (0:2).
• Đồ thị hàm số đi qua điểm (1 ; 6).
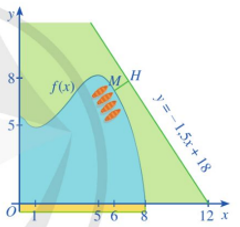
Vậy đồ thị hàm số \[y = f(t) = \frac{{26t + 10}}{{t + 5}},t \ge 0\] thể hiện như hình vẽ dưới đây: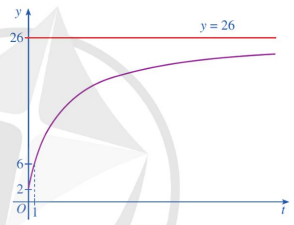
Lời giải
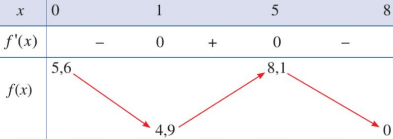
Căn cứ bảng biến thiên, ta có: \[\mathop {\max }\limits_{\left[ {0;8} \right]} \] f(x)= f(5)=8,1 tại x= 5.
c) Xét điểm M(x ; f(x)) thuộc đồ thị hàm số \[y = f(x) = \frac{1}{{10}}( - {x^3} + 9{x^2} - 15x + 56)\] với 0 ≤ x ≤8.
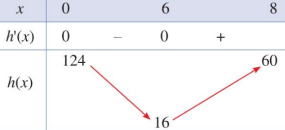
Căn cứ bảng biến thiên, ta có: h(x) > 0 với 0≤x≤8;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.