Để loại bỏ x% chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là \[C(x) = \frac{{300x}}{{100 - x}}\](triệu đồng), 0 ≤ x <100.
Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = C(x). Từ đó, hãy cho biết:
a) Chi phí cần bỏ ra sẽ thay đổi như thế nào khi x tăng?
b) Có thể loại bỏ được 100% chất gây ô nhiễm không khí không? Vì sao?
Để loại bỏ x% chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là \[C(x) = \frac{{300x}}{{100 - x}}\](triệu đồng), 0 ≤ x <100.
Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = C(x). Từ đó, hãy cho biết:
a) Chi phí cần bỏ ra sẽ thay đổi như thế nào khi x tăng?
b) Có thể loại bỏ được 100% chất gây ô nhiễm không khí không? Vì sao?
Quảng cáo
Trả lời:
|
Xét hàm số \[y = C(x) = \frac{{300x}}{{100 - x}},0 \le x < 100\]. |
|
Ta có: \[y' = \frac{{30{\rm{ }}000}}{{{{\left( {100 - x} \right)}^2}}} > 0\], với mọi x \[ \in \] [0; 100). |
|
Do đó hàm số luôn đồng biến trên nửa khoảng [0; 100). |
|
Ta có: \[\mathop {\lim }\limits_{x \to {{100}^ - }} C(x) = \mathop {\lim }\limits_{x \to {{100}^ - }} \frac{{300x}}{{100 - x}} = + \infty \], nên đồ thị hàm số có tiệm cận đứng là x = 100. |
|
Bảng biến thiên: 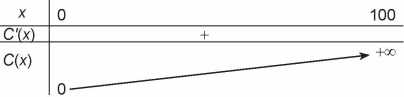 Đồ thị hàm số như Hình 1.34.
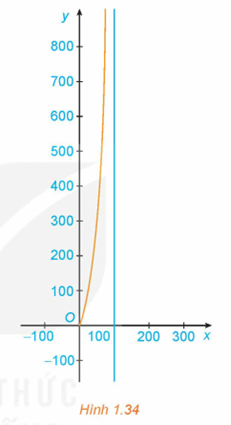 a) Chi phí cần bỏ ra C(x) sẽ luôn tăng khi x tăng. b) Vì \[\mathop {\lim }\limits_{x \to {{100}^ - }} C(x) = + \infty \] (hàm số C(x) không xác định khi x = 100) nên nhà máy không thể loại bỏ 100% chất gây ô nhiễm không khí (dù bỏ ra chi phí là bao nhiêu đi chăng nữa). |
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
2) Đồ thị
• Giao điểm của đồ thị với trục tung: (0:2).
• Đồ thị hàm số đi qua điểm (1 ; 6).
Vậy đồ thị hàm số \[y = f(t) = \frac{{26t + 10}}{{t + 5}},t \ge 0\] thể hiện như hình vẽ dưới đây: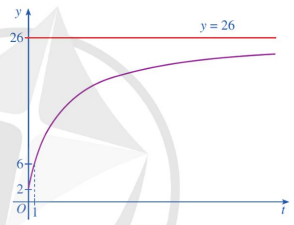
Lời giải
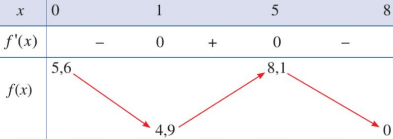
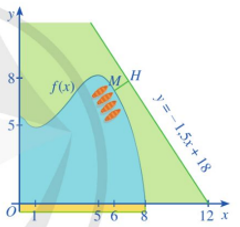
Căn cứ bảng biến thiên, ta có: \[\mathop {\max }\limits_{\left[ {0;8} \right]} \] f(x)= f(5)=8,1 tại x= 5.
c) Xét điểm M(x ; f(x)) thuộc đồ thị hàm số \[y = f(x) = \frac{1}{{10}}( - {x^3} + 9{x^2} - 15x + 56)\] với 0 ≤ x ≤8.
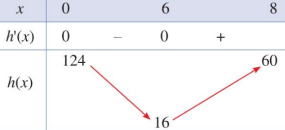
Căn cứ bảng biến thiên, ta có: h(x) > 0 với 0≤x≤8;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.