(Bài toán thiết kế mô hình đường giao thông) Để thiết kế mô hình của một đoạn đường cao tốc nối hai sườn đồi với sự khác biệt về độ cao ở vị trí hai sườn đồi giao nhau là 50 feet (Hình vẽ), người ta có thể làm như sau:
• Chọn hệ trục toạ độ Oxy với gốc O là vị trí hai sườn đồi giao nhau, phương nằm ngang là trục Ox, đơn vị trên mỗi trục toạ độ là feet (1 feet = 0,3048 m).
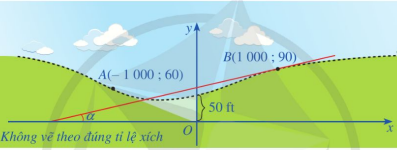
• Chọn hai vị trí A, B lần lượt trên hai sườn đồi. Bằng cách đo đạc tại thực địa, ta xác định được toạ độ của hai điểm A, B và góc dốc a (đơn vị: độ) tại điểm B của sườn đồi. Giả sử ta có A(− 1 000 ; 60), B(1 000 ; 90) và tan\[\alpha \] = 0,04 (Hình 27) (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
• Trong hệ trục toạ độ Oxy, quan sát đường cong (vẽ bằng nét đứt) mô phỏng đoạn đường cao tốc nối hai sườn đồi, đường cong đó gợi nên hình ảnh đồ thị của hàm số bậc ba. Vì thế ta có thể chọn hàm số bậc ba y = f(x) = ax3 + bx2 + cx+d (a ≠ 0) sao cho trong hệ trục toạ độ Oxy, đồ thị của hàm số đó trên đoạn
[− 1 000 ; 1 000] mô phỏng đoạn đường cao tốc cần thiết kế. Ta chọn theo nguyên tắc: Hệ số góc của tiếp tuyến tại B của đồ thị hàm số đó bằng 0,04.
a) Hãy xác định hàm số bậc ba đó.
b) Góc dốc của con đường trên đoạn \[\left[ { - 1000;1000} \right]\] lớn nhất tại điểm nào?
(Bài toán thiết kế mô hình đường giao thông) Để thiết kế mô hình của một đoạn đường cao tốc nối hai sườn đồi với sự khác biệt về độ cao ở vị trí hai sườn đồi giao nhau là 50 feet (Hình vẽ), người ta có thể làm như sau:
• Chọn hệ trục toạ độ Oxy với gốc O là vị trí hai sườn đồi giao nhau, phương nằm ngang là trục Ox, đơn vị trên mỗi trục toạ độ là feet (1 feet = 0,3048 m).
• Chọn hai vị trí A, B lần lượt trên hai sườn đồi. Bằng cách đo đạc tại thực địa, ta xác định được toạ độ của hai điểm A, B và góc dốc a (đơn vị: độ) tại điểm B của sườn đồi. Giả sử ta có A(− 1 000 ; 60), B(1 000 ; 90) và tan\[\alpha \] = 0,04 (Hình 27) (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
• Trong hệ trục toạ độ Oxy, quan sát đường cong (vẽ bằng nét đứt) mô phỏng đoạn đường cao tốc nối hai sườn đồi, đường cong đó gợi nên hình ảnh đồ thị của hàm số bậc ba. Vì thế ta có thể chọn hàm số bậc ba y = f(x) = ax3 + bx2 + cx+d (a ≠ 0) sao cho trong hệ trục toạ độ Oxy, đồ thị của hàm số đó trên đoạn
[− 1 000 ; 1 000] mô phỏng đoạn đường cao tốc cần thiết kế. Ta chọn theo nguyên tắc: Hệ số góc của tiếp tuyến tại B của đồ thị hàm số đó bằng 0,04.

a) Hãy xác định hàm số bậc ba đó.
b) Góc dốc của con đường trên đoạn \[\left[ { - 1000;1000} \right]\] lớn nhất tại điểm nào?
Quảng cáo
Trả lời:
a) Do đồ thị hàm số bậc ba y = f(x) = ax3 + bx2 + cx+d (a ≠ 0) đi qua điểm (0 ; 50) nên d = 50,
suy ra: y = f(x) = ax3 + bx2 + cx + 50.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
2) Đồ thị
• Giao điểm của đồ thị với trục tung: (0:2).
• Đồ thị hàm số đi qua điểm (1 ; 6).
Vậy đồ thị hàm số \[y = f(t) = \frac{{26t + 10}}{{t + 5}},t \ge 0\] thể hiện như hình vẽ dưới đây: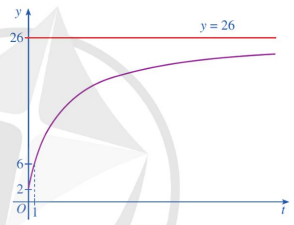
Lời giải
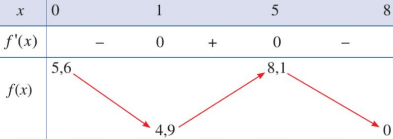
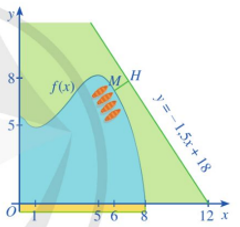
Căn cứ bảng biến thiên, ta có: \[\mathop {\max }\limits_{\left[ {0;8} \right]} \] f(x)= f(5)=8,1 tại x= 5.
c) Xét điểm M(x ; f(x)) thuộc đồ thị hàm số \[y = f(x) = \frac{1}{{10}}( - {x^3} + 9{x^2} - 15x + 56)\] với 0 ≤ x ≤8.
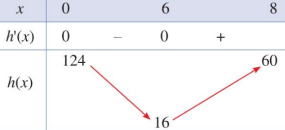
Căn cứ bảng biến thiên, ta có: h(x) > 0 với 0≤x≤8;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.