4 bài tập Tiệm cận ngang (có lời giải)

a) Tiệm cận ngang: \(y = 1\) vì \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{x + 1}}{x} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{1 + \frac{1}{x}}}{1} = 1;\mathop {\lim }\limits_{x \to  - \infty } \frac{{x + 1}}{x} = \mathop {\lim }\limits_{x \to  - \infty } \frac{{1 + \frac{1}{x}}}{1} = 1\).

b) Ta có \(MN = |f(x) - 1| = \left| {\frac{{x + 1}}{x} - 1} \right| = \left| {\frac{1}{x}} \right|\). Và \(\mathop {\lim }\limits_{x \to  + \infty } \left| {\frac{1}{x}} \right| = 0;\mathop {\lim }\limits_{x \to  - \infty } \left| {\frac{1}{x}} \right| = 0.\)

Nhận xét MN tiến dần về 0 khi khi \(x \to  + \infty \) hoặc \(x \to  - \infty \).

TXĐ: \[D = \mathbb{R}\backslash \left\{ { - 1} \right\}\]

Ta có: \[\mathop {\lim }\limits_{x \to  + \infty } \frac{{ - 2x + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{ - 2 + \frac{1}{x}}}{{1 + \frac{1}{x}}} =  - 2;\mathop {\lim }\limits_{x \to  - \infty } \frac{{ - 2x + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to  - \infty } \frac{{ - 2 + \frac{1}{x}}}{{1 + \frac{1}{x}}} =  - 2\]

Vậy đường thẳng \[y =  - 2\] là TCN của đồ thị hàm số đã cho.

a)\(\mathop {\lim }\limits_{x \to  + \infty } f(x) = \mathop {\lim }\limits_{x \to  + \infty } \frac{{x - 1}}{{4x + 1}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{1 - \frac{1}{x}}}{{4 + \frac{1}{x}}} = \frac{1}{4};{\rm{ }}\mathop {\lim }\limits_{x \to  - \infty } f(x) = \mathop {\lim }\limits_{x \to  - \infty } \frac{{x - 1}}{{4x + 1}} = \mathop {\lim }\limits_{x \to  - \infty } \frac{{1 - \frac{1}{x}}}{{4 + \frac{1}{x}}} = \frac{1}{4}.\)

Vậy \(y = \frac{1}{4}\) là tiệm cận ngang của đồ thị hàm số.

b) \(\mathop {\lim }\limits_{x \to  + \infty } g(x) = \mathop {\lim }\limits_{x \to  + \infty } \frac{{\sqrt x }}{{\sqrt x  + 2}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{1}{{1 + \frac{2}{{\sqrt x }}}} = 1;{\rm{ }}\mathop {\lim }\limits_{x \to  - \infty } g(x) = \mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt x }}{{\sqrt x  + 2}} = \mathop {\lim }\limits_{x \to  - \infty } \frac{1}{{1 + \frac{2}{{\sqrt x }}}} = 1.\)

Vậy \({\rm{y}} = 1\) là tiệm cận ngang của đồ thị hàm số.

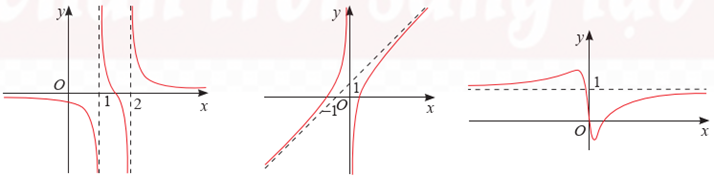
a) Dựa vào đồ thị ta có:

\({\rm{x}} = 1;{\rm{x}} = 2\) là hai tiệm cận đứng của đồ thị hàm số.

\({\rm{y}} = 0\) là tiệm cận ngang của đồ thị hàm số.

b) Dựa vào đồ thị ta có:

\({\rm{x}} = 0\) là tiệm cận đứng của đồ thị hàm số.

\({\rm{y}} = {\rm{x}} + 1\) là tiệm cận xiên của đồ thị hàm số.

c) Dựa vào đồ thị ta có: \({\rm{y}} = 1\) là tiệm cận ngang của đồ thị hàm số.