Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
100 người thi tuần này 4.6 292 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
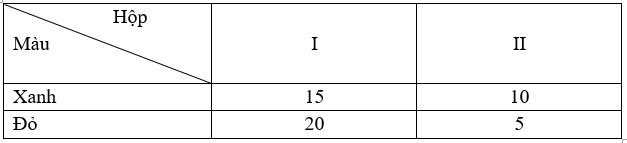
Câu 1
Lời giải
Gọi hai biến cố:
\(A\): “Lấy được bút xanh từ hộp I”;
\(B\): “Lấy được bút xanh từ hộp II”.
Theo bài ra, ta có
\(P\left( A \right) = \frac{{15}}{{20}} = \frac{3}{4}\) ; \(P\left( {\overline A } \right) = 1 - \frac{3}{4} = \frac{1}{4}\) ; \(P\left( {B|A} \right) = \frac{6}{{11}}\) ; \(P\left( {B|\overline A } \right) = \frac{5}{{11}}\).
Áp dụng công thức xác suất toàn phần, ta có
\(P\left( B \right) = P\left( A \right)P\left( {B|A} \right) + P\left( {\overline A } \right)P\left( {B|\overline A } \right) = \frac{3}{4}.\frac{6}{{11}} + \frac{1}{4}.\frac{5}{{11}} = \frac{{23}}{{44}}\).Câu 2
Lời giải
Xét hai biến cố
\(A\): “Chọn được hộp I”;
\(B\): “Chọn được viên bi màu đỏ”
\(P\left( A \right) = \frac{1}{2}\) ; \(P\left( {\overline A } \right) = \frac{1}{2}\) ; \(P\left( {B|A} \right) = \frac{{20}}{{35}} = \frac{4}{7}\) ; \(P\left( {B|\overline A } \right) = \frac{5}{{15}} = \frac{1}{3}\).
Áp dụng công thức xác suất toàn phần, ta có
\(P\left( B \right) = P\left( A \right)P\left( {B|A} \right) + P\left( {\overline A } \right)P\left( {B|\overline A } \right) = \frac{1}{2}.\frac{4}{7} + \frac{1}{2}.\frac{1}{3} = \frac{{19}}{{42}}\).Câu 3
Lời giải
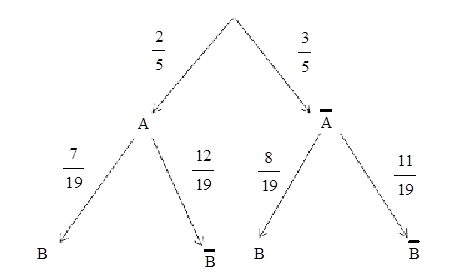
Câu 4
A. \(\frac{{14}}{{95}}\).
Lời giải
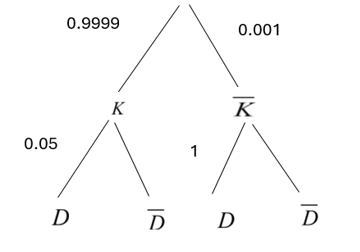
Dựa theo sơ đồ hình cây, ta có
\(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right)P\left( {B|\overline A } \right) = \frac{7}{{19}}.\frac{2}{5} + \frac{8}{{19}}.\frac{3}{5} = \frac{2}{5}\).
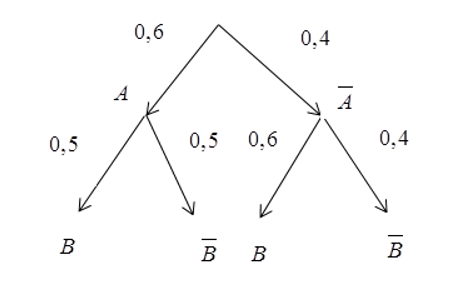
Lời giải
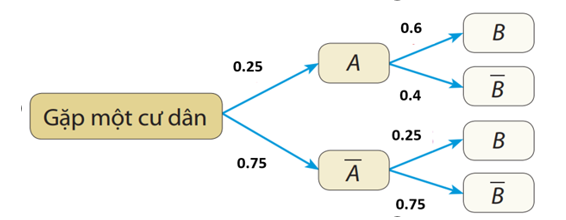
Dựa theo sơ đồ hình cây, ta có
\(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right)P\left( {B|\overline A } \right) = 0,6.0,5 + 0,4.0,6 = 0,54\).Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
a) \(P\left( {B|A} \right) = 0,9\).
b) \(P\left( {\overline B \left| A \right.} \right) = 0,5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
a) Xác suất để vận động viên chọn ra thuộc đội I là \(\frac{5}{9}\)
b) Xác suất không đạt huy chương vàng của mỗi vận động viên đội II là \(0,45\)
c) Xác suất để vận động viên này đạt huy chương vàng là \(\frac{{103}}{{180}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
a) Xác suất chọn được thùng hàng loại I bằng \(48\% \).
b) Xác suất chọn được thùng hàng loại II đã được kiểm định bằng 38,4%.
c) Xác suất chọn được thùng hàng chưa kiểm định bằng 17,4%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
a) Chọn ngẫu nhiên 1 xạ thủ bắn và xạ thủ đó bắn một viên đạn. Gọi A là biến cố “Viên đạn trúng đích”. B là biến cố “ Xạ thủ loại I bắn”. C là biến cố “ Xạ thủ loại II bắn”. Khi đó ta có xác suất để viên đạn trúng đích được tính theo công thức công thức:
\[P\left( A \right) = P\left( B \right)P\left( {A|B} \right) + P\left( C \right).P\left( {A|\overline C } \right)\]
b) Chọn ngẫu nhiên một xạ thủ bắn và xạ thủ đó bắn một viên đạn. Xác suất để viên đạn đó trúng đích là \[0.74\].
c) Chọn ngẫu nhiên ra hai xạ thủ và cả hai xạ thủ đều bắn một viên đạn. Gọi E là biến cố “ Cả hai viên đạn đều bắn trúng đích” \[{E_i}\] là biến cố chọn được i xạ thủ loại I. Khi đó ta có công thức tính xác xuất để cả hai xạ thủ đều bắn trúng là
\[P\left( E \right) = P\left( {{E_o}} \right).P\left( {E|{E_o}} \right) + P\left( {{E_1}} \right).P\left( {E|\overline {{E_1}} } \right) + P\left( {{E_2}} \right).P\left( {E|\overline {{E_2}} } \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.