Một bể chứa ban đầu có 200 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 40 lít nước, đồng thời cho vào bể 20 gam chất khử trùng (hoà tan).
a) Tính thể tích nước và khối lượng chất khử trùng có trong bể sau t phút. Từ đó tính nồng độ chất khử trùng (gam/lít) trong bể sau t phút.
b) Coi nồng độ chất khử trùng là hàm số f(t) với t ≥ 0. Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
c) Hãy giải thích tại sao nồng độ chất khử trùng tăng theo t nhưng không vượt ngưỡng 0,5 gam/lít.
Một bể chứa ban đầu có 200 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 40 lít nước, đồng thời cho vào bể 20 gam chất khử trùng (hoà tan).
a) Tính thể tích nước và khối lượng chất khử trùng có trong bể sau t phút. Từ đó tính nồng độ chất khử trùng (gam/lít) trong bể sau t phút.
b) Coi nồng độ chất khử trùng là hàm số f(t) với t ≥ 0. Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
c) Hãy giải thích tại sao nồng độ chất khử trùng tăng theo t nhưng không vượt ngưỡng 0,5 gam/lít.
Quảng cáo
Trả lời:
a) Thể tích nước có trong bế sau \(t\) phút là: \(V(t) = 200 + 40t\) (lít).
Khối lượng chất khử trùng có trong bế sau t phút là: \({\rm{M}}({\rm{t}}) = 20{\rm{t}}({\rm{gam}})\).
Nồng độ chất khử trùng trong bế sau t phút là: \(\frac{{20t}}{{200 + 40t}}\) (gam/lit).
b) \(y = f(t) = \frac{{20t}}{{200 + 40t}}(t \ge 0)\).
Tập xác định của hàm số là \({\rm{D}} = [0; + \infty )\).
Sự biến thiên:
Ta có \({y^\prime } = \frac{{20(200 + 40t) - 20t \cdot 40}}{{{{(200 + 40t)}^2}}} = \frac{{4000}}{{{{(200 + 40t)}^2}}} > 0\) với mọi \({\rm{t}} \in {\rm{D}}\).
Hàm số luôn đồng biến trên \({\rm{D}}\).
Hàm số không có cực trị.
Tiệm cận:
\(\mathop {\lim }\limits_{t \to + \infty } \frac{{20t}}{{200 + 40t}} = \frac{1}{2}\). Do đó \(y = \frac{1}{2}\) là tiệm cận ngang của đồ thị hàm số (phần bên phải trục Oy).
\(\mathop {\lim }\limits_{t \to {0^ + }} \frac{{20t}}{{200 + 40t}} = 0\)
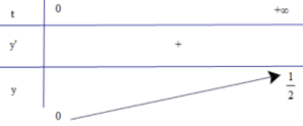
Bảng biến thiên
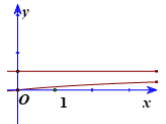
Đồ thị.
Hàm số đi qua điểm \((0;0);\left( {1;\frac{1}{{12}}} \right);\left( {2;\frac{1}{7}} \right)\).
c) Vì \({y^\prime } = \frac{{4000}}{{{{(200 + 40t)}^2}}} > 0,\forall t \ge 0\) và lim \(_{t \to + \infty }\frac{{20t}}{{200 + 40t}} = \frac{1}{2}\) nên nồng độ chất khử trùng tăng theo \(y\) nhưng không vượt ngường \(0,5{\rm{gam}}/\) lít.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
2) Đồ thị
• Giao điểm của đồ thị với trục tung: (0:2).
• Đồ thị hàm số đi qua điểm (1 ; 6).
Vậy đồ thị hàm số \[y = f(t) = \frac{{26t + 10}}{{t + 5}},t \ge 0\] thể hiện như hình vẽ dưới đây: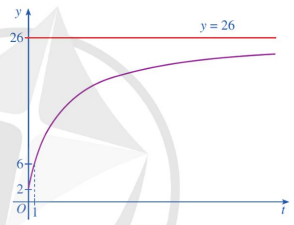
Lời giải
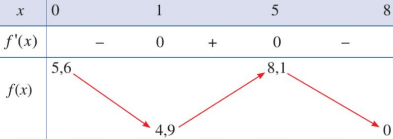
Căn cứ bảng biến thiên, ta có: \[\mathop {\max }\limits_{\left[ {0;8} \right]} \] f(x)= f(5)=8,1 tại x= 5.
c) Xét điểm M(x ; f(x)) thuộc đồ thị hàm số \[y = f(x) = \frac{1}{{10}}( - {x^3} + 9{x^2} - 15x + 56)\] với 0 ≤ x ≤8.
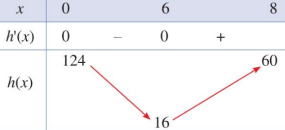
Căn cứ bảng biến thiên, ta có: h(x) > 0 với 0≤x≤8;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.