Cây cà chua khi trồng có chiều cao 5 cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng cho bởi hàm số: \[v(t) = - 0,1{t^3} + {t^2}\]. trong đó t tính theo tuần, v(t) tính bằng centimet/tuần. Gọi h(t) (tính bằng centimet/tuần. Gọi h(t) (tính bằng centimet) là độ cao của cây cà chua ở tuần thứ t.
a) Viết công thức xác định hàm số h(t) \[\left( {t \ge 0} \right)\]
b) Giai đoạn tăng trưởng của cây cà chua đó kéo dài bao lâu?
c) Chiều cao tối đa của cây cà chua đó là bao nhiêu?
d) Vào thời điểm cây cà chua đó phát triền nhanh nhất thì cây cà chua sẽ cao bao nhiêu?
Cây cà chua khi trồng có chiều cao 5 cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng cho bởi hàm số: \[v(t) = - 0,1{t^3} + {t^2}\]. trong đó t tính theo tuần, v(t) tính bằng centimet/tuần. Gọi h(t) (tính bằng centimet/tuần. Gọi h(t) (tính bằng centimet) là độ cao của cây cà chua ở tuần thứ t.
a) Viết công thức xác định hàm số h(t) \[\left( {t \ge 0} \right)\]
b) Giai đoạn tăng trưởng của cây cà chua đó kéo dài bao lâu?
c) Chiều cao tối đa của cây cà chua đó là bao nhiêu?
d) Vào thời điểm cây cà chua đó phát triền nhanh nhất thì cây cà chua sẽ cao bao nhiêu?
Quảng cáo
Trả lời:
a) Hàm số h(t) là một nguyên hàm của hàm số \(v({\rm{t}})\).
Ta có: \(\int v (t)dt = \int {\left( { - 0,1{t^3} + {t^2}} \right)} dt = - 0,1\int {{t^3}} dt + \int {{t^2}} dt = - 0,025{t^4} + \frac{{{t^3}}}{3} + C\)
Suy ra \(h(t) = - 0,025{t^4} + \frac{{{t^3}}}{3} + C\).
Vi cây cà chua khi trồng có chiều cao 5 cm nên \({\rm{h}}(0) = 5\), suy ra \({\rm{C}} = 5\).
Vậy công thức xác định hàm số h(t) là: \(h(t) = - 0,025{t^4} + \frac{{{t^3}}}{3} + 5(t \ge 0)\).
b) Xét hàm số \(h(t) = - 0,025{t^4} + \frac{{{t^3}}}{3} + 5(t \ge 0)\).
Ta có \(h(t) = v(t) = - 0,1{t^3} + {t^2};h(t) = 0\) khi \(t = 0\) hoặc \({\rm{t}} = 10\).
Bảng biến thiên của hàm số \(h(t)\) trên \([0; + \infty )\) như sau:
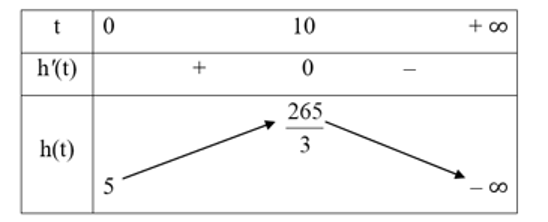
Từ bảng biến thiên ta thấy giai đoạn tăng trưởng của cây cà chua đó kéo dài 10 tuần.
c) Từ bảng biến thiên ở câu b, ta thấy chiều cao tối đa của cây cà chua đó là \(\frac{{265}}{3}\) cm .
d) Xét hàm tốc độ tăng chiều cao của cây cà chua: \(v(t) = - 0,1{t^3} + {t^2}(t \ge 0)\).
Ta có \({v^{\prime \prime }}({\rm{t}}) = - 0,3{{\rm{t}}^2} + 2{\rm{t}};{\rm{v}}\) (t) \( = 0\) khi \({\rm{t}} = 0\) hoặc \({\rm{t}} = \frac{{20}}{3}\).
Bảng biến thiên của hàm số \(v(t)\) trên \([0; + \infty )\) như sau:
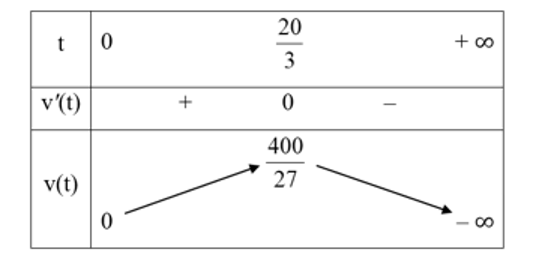
Từ bảng biến thiên ta suy ra vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua cao \(\frac{{400}}{{27}}\;{\rm{cm}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
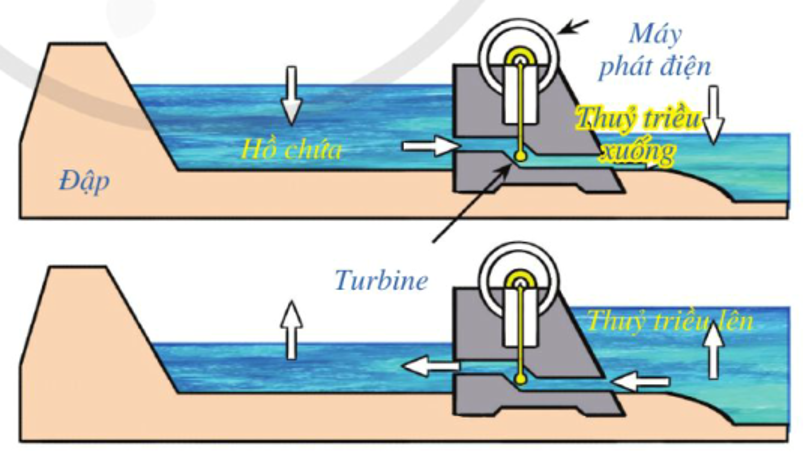
a) Ta có:
\(\begin{array}{l}\int {{h^\prime }} (t){\rm{d}}t = \int {\frac{1}{{216}}} \left( {5{t^2} - 120t + 480} \right){\rm{d}}t = \frac{1}{{216}}\int {\left( {5{t^2} - 120t + 480} \right)} {\rm{d}}t = \frac{5}{{216}}\int {{t^2}} \;{\rm{d}}t - \frac{{120}}{{216}}\int t \;{\rm{d}}t + \frac{{480}}{{216}}\int {\rm{d}} t\\ = \frac{5}{{648}}{t^3} - \frac{5}{{18}}{t^2} + \frac{{20}}{9}t + C\end{array}\)
Suy ra \(h(t) = \frac{5}{{648}}{t^3} - \frac{5}{{18}}{t^2} + \frac{{20}}{9}t + C\).
Tại thời điểm \(t = 0\), mực nước trong hồ chứa là \(6\;{\rm{m}}\) nên \(h(0) = 6\), suy ra \(C = 6\).
Vậy mực nước trong hồ chứa được cho bởi hàm số: \(h(t) = \frac{5}{{648}}{t^3} - \frac{5}{{18}}{t^2} + \frac{{20}}{9}t + 6(0 \le t \le 24)\)
b) Ta tìm \({\min _{[0;24]}}h(t)\) và \({\max _{[0;24]}}h(t)\).
- \({h^\prime }(t) = 0 \Leftrightarrow 5{t^2} - 120t + 480 = 0\)
\( \Leftrightarrow {t^2} - 24t + 96 = 0 \Leftrightarrow t = 12 - 4\sqrt 3 \) hoă̆c \(t = 12 + 4\sqrt 3 \).
- Bảng biến thiên:
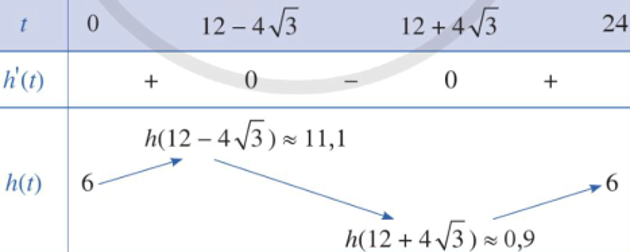
Do đó, ta có: \({\min _{[0;24]}}h(t) = \min \{ h(0);h(12 + 4\sqrt 3 )\} = h(12 + 4\sqrt 3 ) \approx 0,9\);
\({\max _{[0;24]}}h(t) = \max \{ h(24);h(12 - 4\sqrt 3 )\} = h(12 - 4\sqrt 3 ) \approx 11,1\)
Vậy mực nước trong hồ chứa cao nhất khoảng \(11,1\;{\rm{m}}\) và thấp nhất khoảng \(0,9\;{\rm{m}}\).
c) Ta tìm \({\max _{[0;24]}}{h^\prime }(t)\).
- \({h^{\prime \prime }}(t) = \frac{1}{{216}}(10t - 120)\);
\({h^{\prime \prime }}(t) = 0{\rm{ khi }}t = 12.{\rm{ }}\)
- Bảng biến thiên của hàm số \({h^\prime }(t)\) :
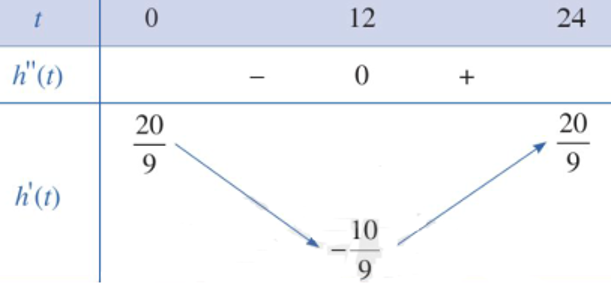
Do đó, ta có: \({\max _{[0;24]}}{h^\prime }(t) = \max \left\{ {{h^\prime }(0);{h^\prime }(24)} \right\} = {h^\prime }(24) = \frac{{20}}{9}\).
Vậy mực nước trong hồ chứa thay đổi nhanh nhất khi \(t = 0\) và \(t = 24\). Tốc độ thay đổi của mực nước trong hồ chứa khi đó là \(\frac{{20}}{9}\;{\rm{m}}/{\rm{h}}\).
Lời giải
a) Hàm số \({\rm{B}}({\rm{t}})\) là một nguyên hàm của hàm số \(B(t)\).
Ta có \(\int {{B^\prime }} (t)dt = \int {\left( {20{t^3} - 300{t^2} + 1000t} \right)} dt\)\( = \int 2 0{t^3}dt - \int 3 00{t^2}dt + \int 1 000tdt.\)
Suy ra \(B(t) = 5{t^4} - 100{t^3} + 500{t^2} + C\).
Vì sau một giờ, 500 người đã có mặt tại lễ hội nên \(B(1) = 500\).
Do đó, \(5 \cdot {1^4} - 100 \cdot {1^3} + 500 \cdot {1^2} + C = 500\), suy ra \(C = 95\).
Vậy công thức của hàm số \({\rm{B}}({\rm{t}})\) biểu diễn số lượng khách tham dự lễ hội là
\(B(t) = 5{t^4} - 100{t^3} + 500{t^2} + 95(0 \le t \le 15).\)
b) Ta có \(B(3) = 5 \cdot {3^4} - 100 \cdot {3^3} + 500 \cdot {3^2} + 95 = 2300\).
Vậy sau 3 giờ có 2300 khách tham dự lễ hội.
c) Số lượng khách tham dự lễ hội lớn nhất chính là giá trị lớn nhất của hàm số \({\rm{B}}({\rm{t}})\) trên đoạn [0;15].
Ta có \({B^\prime }({\rm{t}}) = 20{{\rm{t}}^3} - 300{{\rm{t}}^2} + 1000{\rm{t}}\).
Trên khoảng \((0;15),{B^\prime }({\rm{t}}) = 0\) khi \(t = 5\) hoặc \({\rm{t}} = 10\).
\(B(0) = 95;B(5) = 3220;B(10) = 95;B(15) = 28220.{\rm{ }}\)
Do đó, \({\max _{[0;15]}}B(t) = 28220\) tại \(t = 15\).
Vậy số lượng khách tham dự lễ hội lớn nhất là 28220 khách sau 15 giờ.
d) Tốc độ thay đổi lượng khách tham dự lễ hội lớn nhất chính là giá trị lớn nhất của hàm số \({B^\prime }({\rm{t}})\) trên đoạn [0 ; 15].
Ta có \({B^{\prime \prime }}(t) = {\left( {20{t^3} - 300{t^2} + 1000t} \right)^\prime } = 60{t^2} - 600t + 1000\).
Trên khoảng \((0;15),{{\rm{B}}^{\prime \prime }}({\rm{t}}) = 0\) khi \(t = \frac{{15 - 5\sqrt 3 }}{3}\) hoặc \(t = \frac{{15 + 5\sqrt 3 }}{3}\).
\({{\rm{B}}^\prime }(0) = 0;B\left( {\frac{{15 - 5\sqrt 3 }}{3}} \right) \approx 962,25;B\left( {\frac{{15 + 5\sqrt 3 }}{3}} \right) \approx - 962,25;{\rm{B}}(15) = 15000.{\rm{ }}\)
Do đó, \({\max _{[0;15]}}{B^\prime }(t) = 15000\) tại \(t = 15\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.