Cho hàm số \(y = \frac{{2x + 3}}{{x - 1}}\) có đồ thị (C). Chọn đáp án đúng.
Cho hàm số \(y = \frac{{2x + 3}}{{x - 1}}\) có đồ thị (C). Chọn đáp án đúng.
A. Đồ thị hàm số (C) nhận đường thẳng x = 2 là tiệm cận ngang;
B. Đồ thị hàm số (C) nhận I(2; 3) là tâm đối xứng;
C. Tiếp tuyến của (C) tại giao điểm của (C) với Oy có phương trình y = −5x – 3;
D. Tích khoảng cách từ một điểm bất kỳ trên (C) tới 2 đường tiệm cận của nó luôn bằng 3.
Quảng cáo
Trả lời:
Đáp án đúng là: C
Tiệm cận ngang của (C) là đường thẳng y = 2 vì \(\mathop {\lim }\limits_{x \to \pm \infty } \frac{{2x + 3}}{{x - 1}} = 2\).
Đồ thị (C) có 2 đường tiệm cận là x = 1 và y = 2 nên tâm đối xứng của (C) là điểm I(1; 2).
Giao điểm của (C) với Oy là điểm A(0; −3).
Ta có \(y = \frac{{2x + 3}}{{x - 1}} \Rightarrow y' = \frac{{ - 5}}{{{{\left( {x - 1} \right)}^2}}} \Rightarrow y'\left( 0 \right) = - 5\).
Phương trình tiếp tuyến của (C) tại A(0; −3) là y = y'(0)(x − 0) + (−3) y = −5x – 3.
Gọi M(x0; y0) là một điểm bất kỳ trên (C), suy ra \({y_0} = \frac{{2{x_0} + 3}}{{{x_0} - 1}}\).
Đồ thị (C) có 2 đường tiệm cận là ∆1: x – 1 = 0 và ∆2: y – 2 = 0.
Khoảng cách từ M(x0; y0) tới ∆1: x – 1 = 0 là d1 = |x0 – 1|.
Khoảng cách từ M(x0; y0) tới ∆2: y – 2 = 0 là
\({d_2} = \left| {{y_0} - 2} \right| = \left| {\frac{{2{x_0} + 3}}{{{x_0} - 1}} - 2} \right| = \left| {\frac{5}{{{x_0} - 1}}} \right| = \frac{5}{{\left| {{x_0} - 1} \right|}}\).
Suy ra \[{d_1}.{d_2} = \left| {{x_0} - 1} \right|.\frac{5}{{\left| {{x_0} - 1} \right|}} = 5\] .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải:
1) Tập xác định: ℝ.
2) Sự biến thiên
Ta có y' = 3x2 – 6x; y' = 0 3x2 – 6x = 0 x = 0 hoặc x = 2.
Hàm số đồng biến trên mỗi khoảng (−∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại x = 0; yCĐ = 4 ; hàm số đạt cực tiểu tại x = 2; yCT = 0.
Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \).
Bảng biến thiên:
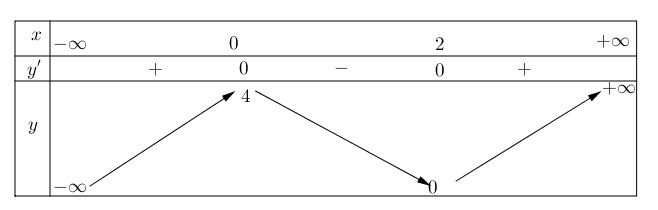
3) Đồ thị
- Giao điểm của đồ thị với trục tung: (0; 4).
- Giao điểm của đồ thị với trục hoành:
Xét phương trình x3 – 3x2 + 4 = 0 x = −1 hoặc x = 2.
Vậy đồ thị hàm số giao với trục hoành tại hai điểm (−1; 0) và (2; 0).
- Đồ thị hàm số đi qua các điểm (−1; 0), (2; 0), (0; 4) và (1; 2).
Vậy đồ thị hàm số y = x3 – 3x2 + 4 được cho ở Hình.
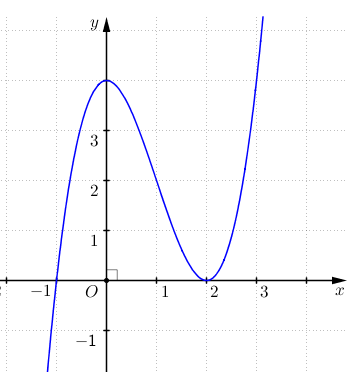
Quan sát đồ thị ở Hình, ta thấy đồ thị đó có tâm đối xứng là điểm I(1; 2).
Câu 2
A. 0;
B. 1;
C. 2;
D. −2.
Lời giải
Đáp án đúng là: C
Gọi M(x0; y0) là giao điểm của đồ thị hàm số với trục tung.
Ta có x0 = 0 y0 = 2.
Câu 3
A. (C) cắt trục hoành tại hai điểm;
B. (C) cắt trục hoành tại một điểm;
C. (C) không cắt trục hoành;
D. (C) cắt trục hoành tại ba điểm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Tâm đối xứng là I(1; 3);
B. Tiệm cận đứng là đường thẳng x = 1;
C. Tiệm cận xiên là đường thẳng y = x + 3;
D. Đồ thị hàm số đi qua điểm A(2; 6).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Tập xác định của hàm số f(x) là D = ℝ\{−1};
B. Hàm số f(x) nghịch biến trên từng khoảng xác định của nó;
C. Đường thẳng y = x + 3 là đường tiệm cận xiên của (C);
D. Điểm I(−1; −1) là tâm đối xứng của đồ thị hàm số.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
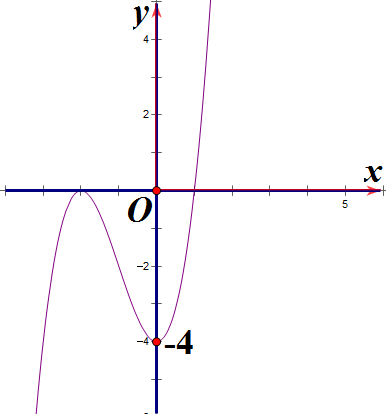
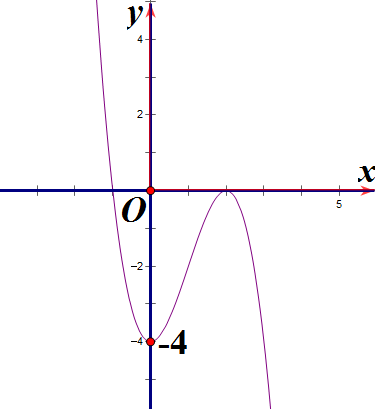
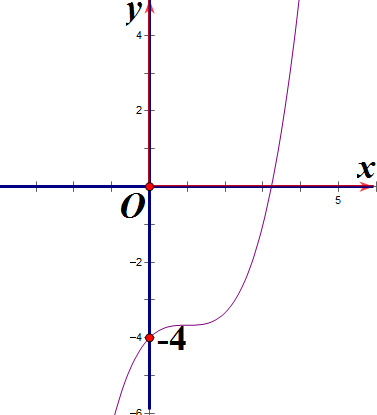
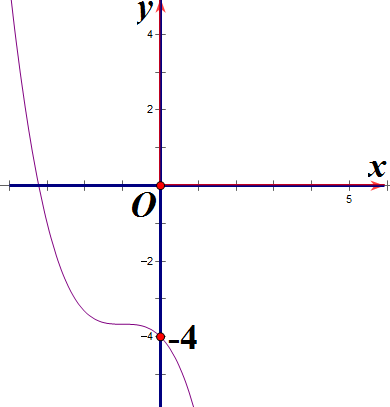
Hàm số y = x3 + 3x2 – 4 có đồ thị là hình nào sau đây?
|
|
|
|
Hình 1 | Hình 2 | Hình 3 | Hình 4 |
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.