khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

19/08/2025 760 Lưu

Cho hình chóp S.ABCD. Gọi I là trọng tâm của tam giác ABC và J là trọng tâm tam giác ADC. Chứng minh rằng: \[2\overrightarrow {SA}  + \overrightarrow {SB}  + 2\overrightarrow {SC}  + \overrightarrow {SD} \; = 3(\overrightarrow {SI} \; + \overrightarrow {SJ} )\].

Xem lời giải

Câu hỏi trong đề: Các dạng bài tập Vectơ trong không gian lớp 12 (có lời giải) !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack
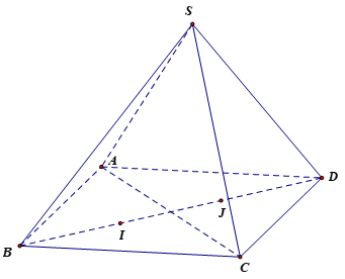
Cho hình chóp S.ABCD. Gọi I là trọng tâm của tam giác ABC và J là trọng tâm tam giác ADC. (ảnh 1)

Vì \({\rm{I}}\) là trọng tâm của \({\rm{DABC}}\) nên \(\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  = \vec 0\)

\( \Leftrightarrow \overrightarrow {SA}  - \overrightarrow {SI}  + \overrightarrow {SB}  - \overrightarrow {SI}  + \overrightarrow {SC}  - \overrightarrow {SI}  = \vec 0 \Leftrightarrow \overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  = 3\overrightarrow {SI} (1).\)Tương tự, \(\overrightarrow {SA}  + \overrightarrow {SD}  + \overrightarrow {SC}  = 3\overrightarrow {SJ} \) (2).

Cộng từng vế (1) và (2), ta có: \(2\overrightarrow {SA}  + \overrightarrow {SB}  + 2\overrightarrow {SC}  + \overrightarrow {SD}  = 3(SI + \overrightarrow {SJ} )\).

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC; G là trọng tâm của tam giác BCD. Chứng minh rằng:
Media VietJack

a) \[\overrightarrow {MN}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {DC} } \right)\]

b) \[\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = 3\overrightarrow {AG} \]

Lời giải

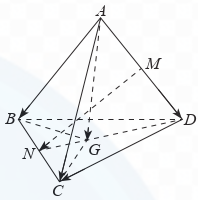
a) Ta có: \(\overrightarrow {MN}  = \overrightarrow {MA}  + \overrightarrow {AB}  + \overrightarrow {BN} ,\overrightarrow {MN}  = \overrightarrow {MD}  + \overrightarrow {DC}  + \overrightarrow {CN} \).

Do đó \(2\overrightarrow {MN}  = \overrightarrow {MA}  + \overrightarrow {MD}  + \overrightarrow {AB}  + \overrightarrow {DC}  + \overrightarrow {BN}  + \overrightarrow {CN} \).

Vì \(M\) là trung điểm của đoạn thẳng AD nên \(\overrightarrow {MA}  + \overrightarrow {MD}  = \vec 0\).

Vì \(N\) là trung diểm của đoạn thẳng BC nên \(\overrightarrow {BN}  + \overrightarrow {CN}  = \vec 0\).

Do đó \(\overrightarrow {MN}  = \frac{1}{2}(\overrightarrow {AB}  + \overrightarrow {DC} )\).

b) Ta có: \(\overrightarrow {AB}  = \overrightarrow {AG}  + \overrightarrow {GB} ,\overrightarrow {AC}  = \overrightarrow {AG}  + \overrightarrow {GC} ,\overrightarrow {AD}  = \overrightarrow {AG}  + \overrightarrow {GD} \).

Suy ra \(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = 3\overrightarrow {AG}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD} \).

Vì \(G\) là trọng tâm của tam giác BCD nên \(\overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \vec 0\).

Do đó \(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = 3\overrightarrow {AG} \).

Câu 2

Cho hình hộp ABCD.EFGH. Điểm M  là trọng tâm của tam giác AFH (Hình 2.16).

a) Tìm \[\overrightarrow u  = \overrightarrow {AB}  + \overrightarrow {CB}  + \overrightarrow {GH}  + \overrightarrow {EH} \]                              

b) Tìm \[\overrightarrow v  = \overrightarrow {FA}  - \overrightarrow {BD} \]

c) Chứng minh rằng ba điểm E, M, C thẳng hàng.

d) Tính độ dài của \[\overrightarrow {EM} \] trong trường hợp ABCD.EFGH là hình hộp đứng có các cạnh AB = 5, AD = 6,  AE = 10 và \[\widehat {ABC}\] = 120°.

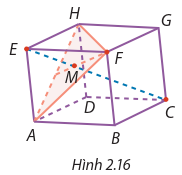
Cho hình hộp ABCD.EFGH. Điểm M là trọng tâm của tam giác AFH (Hình 2.16). (ảnh 1)

Lời giải

c) Để chứng minh E, M, C thẳng hàng, ta sẽ chứng minh \[\overrightarrow {EC}  = k\overrightarrow {EM} \] với k là một số thực nào đó. 
Do M là trọng tâm của tam giác AFH nên ta có: \[\overrightarrow {EA}  + \overrightarrow {EF}  + \overrightarrow {EH}  = 3\overrightarrow {EM} \]
Mặt khác, theo quy tắc hình hộp thì: \[\overrightarrow {EA}  + \overrightarrow {EF}  + \overrightarrow {EH}  = \overrightarrow {EC} \] 
Suy ra \[\overrightarrow {EC}  = 3\overrightarrow {EM} \]. Vậy ba điểm E, M, C thẳng hàng. 
d) Áp dụng định lí côsin trong tam giác ABC, ta có: AC2 = 52 + 62 − 2.5.6.cos 120° = 91.

Khi ABCD.EFGH là hình hộp đứng thì EAC là tam giác vuông tại A, do đó:

EC2 = EA2 + AC2 = 100 + 91 = 191. Suy ra EM = \[EM = \frac{1}{3}\sqrt {191} \].

Câu 3

Cho tứ diện ABCD có G là trọng tâm của tam giác BCD. Gọi H, K lần lượt là trung điểm của các cạnh AB, AC. Chứng minh rằng:

a) \[\overrightarrow {BC}  = 2\overrightarrow {HK} \];

b) \[\overrightarrow {AB}  + {\rm{ }}\overrightarrow {AC}  + \overrightarrow {AD}  = 3\overrightarrow {AG} \].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình lăng trụ ABC.A′B′C′ có M là trung điểm của BB′ . Đặt \[\overrightarrow {CA}  = \overrightarrow a ,\overrightarrow {CB}  = {\overrightarrow b _,}\overrightarrow {CC'} \; = {\overrightarrow c _.}\]. Chứng minh rằng: \[\overrightarrow {AM}  = \overrightarrow b  - \overrightarrow a  + \frac{1}{2}{\overrightarrow c _.}\]
 

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình hộp ABCD. A′B′C′D′ có AC′ và A′C cắt nhau tại O (Hình vẽ)

Cho hình hộp ABCD. A′B′C′D′ có AC′ và A′C cắt nhau tại O (Hình vẽ) (ảnh 1)

a) Tìm vec tơ \[\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'} \].

b) Cho biết mối quan hệ giữa vec tơ tìm được ở câu a) và vec tơ \[\overrightarrow {AO} \].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập