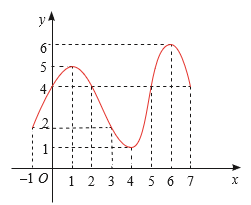
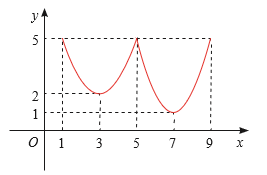
Tìm cực trị của hàm số y = f (x) có đồ thị được cho ở Hình vẽ

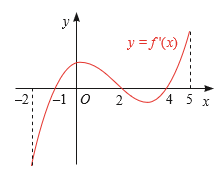
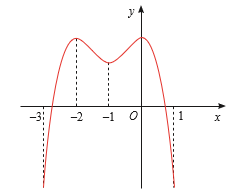
\({f^\prime }(x) > 0\) trên các khoảng \(( - 1;2)\) và \((4;5)\) nên \({f^\prime }(x)\) đồng biến trên các khoảng \(( - 1;2)\) và \((4;5)\) \({{\rm{f}}^\prime }({\rm{x}}) < 0\) trên các khoảng \(( - 2; - 1)\) và \((2;4)\) nên \({{\rm{f}}^\prime }({\rm{x}})\) nghịch biến trên các khoảng \(( - 2; - 1)\) và \((2;4)\)

Ta có: \({f^\prime }(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{x = 2}\\{x = 4}\end{array}} \right.\)

Vậy \(f(x)\) đạt cực tiểu tại \(x = - 1\) và \(x = 4\) do \({f^\prime }(x)\) đổi dấu từ âm sang dương khi đi qua \(x = - 1\) và \(x = 4\), đạt cực đại tại \(x = 2\) do \({f^\prime }(x)\) dổi dấu từ dương sang âm khi đi qua \(x = 2\)

a) Hàm số đồng biến trên khoảng \((0; + \infty )\); Hàm số nghịch biến trên khoảng \(( - \infty ;0)\)

b) \({{\rm{f}}^\prime }({\rm{x}}) = {\left( {{x^2}} \right)^\prime } = 2{\rm{x}}\). Ta có: \({{\rm{f}}^\prime }({\rm{x}}) > 0 \Leftrightarrow 2x > 0 \Leftrightarrow x > 0\); \({{\rm{f}}^\prime }({\rm{x}}) < 0 \Leftrightarrow 2x < 0 \Leftrightarrow x < 0\)

c) Nhận xét:

\({{\rm{f}}^\prime }({\rm{x}}) > 0\) trên \(K\) thì \(y = f(x)\) đồng biến trên \(K\)

\({{\rm{f}}^\prime }({\rm{x}}) < 0\) trên \({\rm{K}}\) thì \({\rm{y}} = {\rm{f}}({\rm{x}})\) nghịch biến trên \({\rm{K}}\)