Trong tất cả các hình chữ nhật có cùng diện tích 48 cm2, hình chữ nhật có chu vi nhỏ nhất bằng:
A. \(16\sqrt 3 \) cm;
B. \(4\sqrt 3 \)cm;
C. 24 cm;
D. \(8\sqrt 3 \)cm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
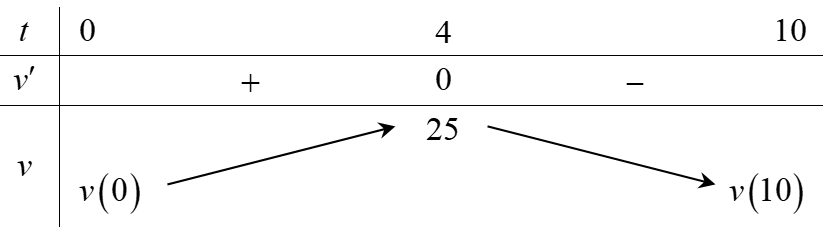
Gọi cạnh của hình chữ nhật: a, b; 0 < a, b 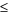48
Ta có: \(ab = 48 \Leftrightarrow b = \frac{{48}}{a}\). Chu vi: \(P\left( a \right) = 2\left( {a + \frac{{48}}{a}} \right)\).
Có \[P'\left( a \right) = 2\left( {1 - \frac{{48}}{{{a^2}}}} \right);P'\left( a \right) = 0 \Leftrightarrow a = 4\sqrt 3 \].
Bảng biến thiên:
Vậy hình chữ nhật có chu vi nhỏ nhất là \(16\sqrt 3 \).
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
Gọi độ dài cạnh đáy và chiều cao hộp quà lần lượt là x (cm) và y (cm) (x > 0, y > 0).
Theo giả thiết, ta có: 2x2 + 4xy = 200 \( \Rightarrow y = \frac{{50}}{x} - \frac{x}{2}\) và x < 10 (vì y > 0).
Xét hàm số \(V(x) = {x^2}\left( {\frac{{50}}{x} - \frac{x}{2}} \right) = 50x - \frac{1}{2}{x^3}\left( {0 < x < 10} \right)\) là thể tích của hộp quà mà bạn Hoa gấp được.
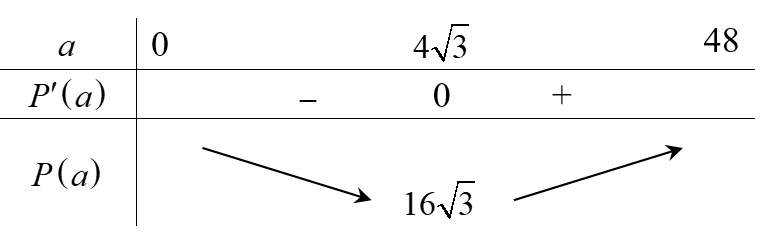
Ta có: \(V'\left( x \right) = 50 - \frac{3}{2}{x^2} = 0 \Leftrightarrow x = \pm \sqrt {\frac{{100}}{3}} \).
Bảng biến thiên của hàm số V(x) là:
Vậy bạn Hoa có thể gấp hộp quà có thể tích lớn nhất là \(V\left( {\sqrt {\frac{{100}}{3}} } \right) \approx 192(c{m^3}).\)
Câu 2
A. 88 m/s;
B. 25 m/s;
C. 100 m/s;
D. 11 m/s.
Lời giải
Đáp án đúng là: B
Ta có v = S' = −t2 + 8t + 9, t ∈ (0; 10).
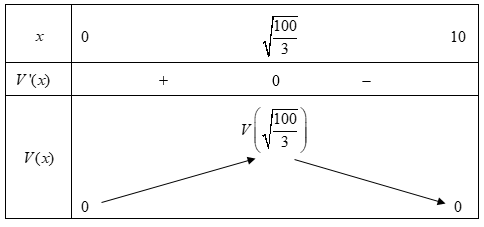
Có v' = −2t + 8; v' = 0 t = 4 ∈ (0; 10).
Bảng biến thiên:
Vậy vận tốc lớn nhất của chất điểm là 25 m/s tại t = 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. t = 2;
B. t = 1;
C. t = 3;
D. t = 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 4 giờ;
B. 1 giờ;
C. 3 giờ;
D. 2 giờ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 243 (m/s);
B. 27 (m/s);
C. 144 (m/s);
D. 36 (m/s).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập