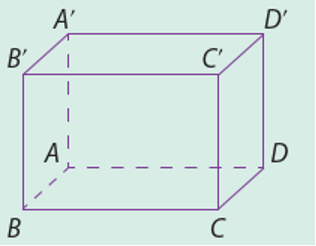
Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\).
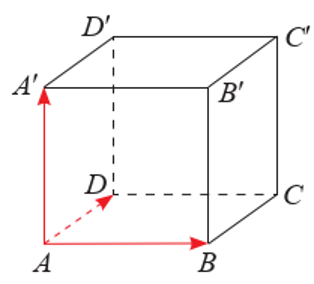
a) Tìm một cặp vectơ chỉ phương của mặt phẳng \((ABCD)\).
b) Tìm một vectơ pháp tuyến của mặt phẳng \((ABCD)\).
Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\).
a) Tìm một cặp vectơ chỉ phương của mặt phẳng \((ABCD)\).
b) Tìm một vectơ pháp tuyến của mặt phẳng \((ABCD)\).
Câu hỏi trong đề: Các dạng bài tập Phương trình mặt phẳng lớp 12 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Vì \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) không cùng phương và có giá nằm trong mặt phẳng \((ABCD)\) nên \(\overrightarrow {AB} ,\overrightarrow {AD} \) là một cặp vectơ chỉ phương của \((ABCD)\).
b) Vì \(A{A^\prime } \bot (ABCD)\) nên \(\overrightarrow {A{A^\prime }} \) là một vectơ pháp tuyến của \((ABCD)\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Một vectơ pháp tuyến của mặt phẳng \((P)\) là: \(\vec n = [\vec a,\vec b]{\rm{ }} = \left( {\left| {\begin{array}{*{20}{c}}3&5\\{ - 1}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}5&1\\1&{ - 3}\end{array}} \right|;{\rm{ }}\left| {{\mkern 1mu} \begin{array}{*{20}{c}}1&3\\{ - 3}&{ - 1}\end{array}} \right|} \right) = (8; - 16;8).\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Ta có \(\quad \vec M = [\overrightarrow {OP} ,\vec F] = \left( {\left| {\begin{array}{*{20}{l}}y&z\\b&c\end{array}} \right|;\left| {\begin{array}{*{20}{l}}z&x\\c&a\end{array}} \right|;\left| {\begin{array}{*{20}{l}}x&y\\a&b\end{array}} \right|} \right)\) \( = (yc - bz;za - cx;bx - ay)\)
b) Vì \(\overrightarrow {O{P^\prime }} = 2\overrightarrow {OP} \) nên \(2\overrightarrow {OP} = (2x;2y;2z)\)
Khi đó \(\overrightarrow {{M^\prime }} = \left[ {\overrightarrow {O{P^\prime }} ,\vec F} \right] = \left( {\left| {\begin{array}{*{20}{c}}{2y}&{2z}\\b&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2z}&{2x}\\c&a\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2x}&{2y}\\a&b\end{array}} \right|} \right){\rm{ }}\)\( = (2yc - b2z;2za - 2cx;2bx - 2ay)\)
Suy ra \(\overrightarrow {{M^\prime }} = 2\vec M\).
Vậy giữ nguyên lực tác động \(\vec F\) trong khi thay vị trí đặt lực từ P sang \({{\rm{P}}^\prime }\) sao cho \(\overrightarrow {O{P^\prime }} = 2\overrightarrow {OP} \) thì moment lực sẽ tăng lên gấp đôi.
Kết luận: Từ kết quả trên, ta có thể rút ra rằng để đỡ tốn sức khi dùng mỏ lết vặn ốc, ta nên tăng khoảng cách từ điểm tác dụng lực đến trục quay (điểm O ).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập