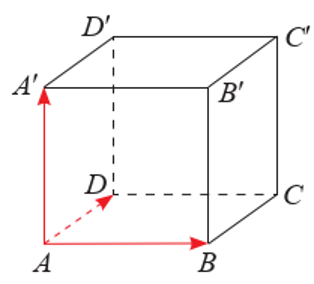
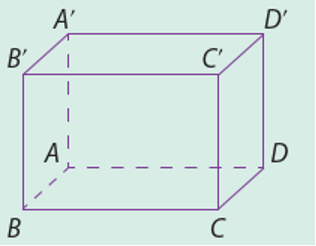
Cho hình lập phương \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\).

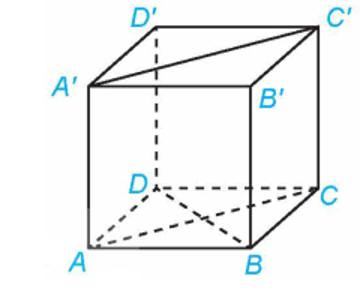
Trong các khẳng định sau, những khẳng định nào là đúng?

a) \(\overrightarrow {A{A^\prime }} \) và \(2\overrightarrow {B{B^\prime }} \) đều là vectơ pháp tuyến của mặt phẳng \((ABCD)\).

b) \(\overrightarrow {BD} \) là một vectơ pháp tuyến của mặt phẳng (ACC'A).

c) \(\overline {{A^\prime }{C^\prime }} \) là một vectơ pháp tuyến của mặt phẳng (ABCD).

Một vectơ pháp tuyến của mặt phẳng \((P)\) là: \(\vec n = [\vec a,\vec b]{\rm{ }} = \left( {\left| {\begin{array}{*{20}{c}}3&5\\{ - 1}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}5&1\\1&{ - 3}\end{array}} \right|;{\rm{ }}\left| {{\mkern 1mu} \begin{array}{*{20}{c}}1&3\\{ - 3}&{ - 1}\end{array}} \right|} \right) = (8; - 16;8).\)

Bốn vectơ pháp tuyến của mặt phẳng \(\left( {A{A^\prime }{B^\prime }B} \right)\) là: \(\overrightarrow {AD} ,\overrightarrow {{A^\prime }{D^\prime }} ,\overrightarrow {BC} ,\overrightarrow {{B^\prime }{C^\prime }} \). Hai cặp vectơ chỉ phương của mặt phẳng \(\left( {A{A^\prime }{B^\prime }B} \right)\) là: \(\overrightarrow {AB} ,\overrightarrow {A{A^\prime }} \) và \(\overrightarrow {AB} ,\overrightarrow {A{B^\prime }} \).