Kim tự tháp Kheops ở Ai Câpp có dạng hình chóp S.ABCD, có đáy là hình vuông với cạnh dài 230 m , các cạnh bên bằng nhau và dài 219 m (theo britannica.com) (H.5.38). Tính góc giữa hai mặt phẳng \((SAB)\) và (SBC).

Kim tự tháp Kheops ở Ai Câpp có dạng hình chóp S.ABCD, có đáy là hình vuông với cạnh dài 230 m , các cạnh bên bằng nhau và dài 219 m (theo britannica.com) (H.5.38). Tính góc giữa hai mặt phẳng \((SAB)\) và (SBC).

Quảng cáo
Trả lời:
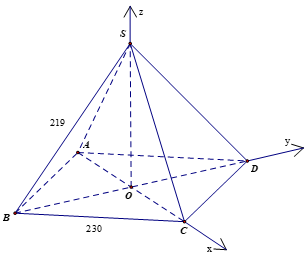
Gọi O là giao điểm của AC và BD . Suy ra O là trung điếm của \({\rm{AC}},{\rm{BD}}\).
Vì các tam giác SAC, SBD đều cân tại S, SO là trung tuyến nên SO đồng thời là đường cao.
Suy ra \(SO \bot AC\), \(SO \bot BD\) nên \(SO \bot (ABCD)\).
Chọn hệ tọa độ như hình vẽ.
Vi ABCD là hình vuông cạnh 230 m nên \({\rm{OA}} = {\rm{OB}} = {\rm{OC}} = {\rm{OD}} = 115\sqrt 2 \).
Xét tam giác SOB vuông tại \(O\), có \(SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {{{219}^2} - {{(115\sqrt 2 )}^2}} = 7\sqrt {439} \)
Ta có \(A( - 115\sqrt 2 ;0;0),B(0; - 115\sqrt 2 ;0),C(115\sqrt 2 ;0;0),S(0;0;7\sqrt {439} )\)
Ta có \(\overrightarrow {SA} = ( - 115\sqrt 2 ;0; - 7\sqrt {439} ),\overrightarrow {SB} = (0; - 115\sqrt 2 ; - 7\sqrt {439} )\),
\(\begin{array}{l}\overrightarrow {SC} = (115\sqrt 2 ;0; - 7\sqrt {439} )\\{\rm{Ta c\'o }}[\overrightarrow {SA} ,\overrightarrow {SB} ] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - 7\sqrt {439} }\\{ - 115\sqrt 2 }&{ - 7\sqrt {439} }\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - 7\sqrt {439} }&{ - 115\sqrt 2 }\\{ - 7\sqrt {439} }&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - 115\sqrt 2 }&0\\0&{ - 115\sqrt 2 }\end{array}} \right|} \right)\\ = ( - 805\sqrt {878} ; - 805\sqrt {878} ;26450)\end{array}\)
\([\overrightarrow {SB} ,\overrightarrow {SC} ] = \left( {\left| {\begin{array}{*{20}{c}}{ - 115\sqrt 2 }&{ - 7\sqrt {439} }\\0&{ - 7\sqrt {439} }\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - 7\sqrt {439} }&0\\{ - 7\sqrt {439} }&{115\sqrt 2 }\end{array}} \right|,\left| {\begin{array}{*{20}{c}}0&{ - 115\sqrt 2 }\\{115\sqrt 2 }&0\end{array}} \right|} \right) = (805\sqrt {878} ; - 805\sqrt {878} ;26450)\)
Mặt phắng (SAB) nhận \(\vec n = \frac{1}{5}[\overrightarrow {SA} ,\overrightarrow {SB} ] = ( - 161\sqrt {878} ; - 161\sqrt {878} ;5290)\) làm vectơ pháp tuyến.
Mặt phắng (SBC) nhận \(\overrightarrow {{n^\prime }} = \frac{1}{5}[\overrightarrow {SB} ,\overrightarrow {SC} ] = (161\sqrt {878} ; - 161\sqrt {878} ;5290)\) làm vectơ pháp tuyến.
Do đó
\(\begin{array}{l}\cos ((SAB),(SBC)) = \frac{{\left| { - {{(161\sqrt {878} )}^2} + {{(161\sqrt {878} )}^2} + {{5290}^2}} \right|}}{{\sqrt {{{( - 161\sqrt {878} )}^2} + {{( - 161\sqrt {878} )}^2} + {{5290}^2}} \cdot \sqrt {{{(161\sqrt {878} )}^2} + {{( - 161\sqrt {878} )}^2} + {{5290}^2}} }}\\ = \frac{{{{5290}^2}}}{{{{(161\sqrt {878} )}^2} + {{( - 161\sqrt {878} )}^2} + {{5290}^2}}} \approx 0,3807\end{array}\)
Suy ra . Vậy góc giữa hai mặt phắng (SAB) và (SBC) khoảngHot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
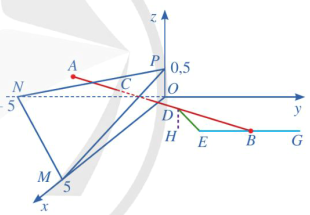
a) Đường thẳng AB đi qua điếm \({\rm{A}}(3,5; - 2;0,4)\) và nhận \(\overrightarrow {AB} = (0;7,5; - 0,4)\) làm vectơ chỉ phương.
Phương trình tham số của đường thắng AB là: \(\left\{ {\begin{array}{*{20}{l}}{x = 3,5}\\{y = - 2 + 7,5t{\rm{ (t là tham số)}}{\rm{. }}}\\{z = 0,4 - 0,4t}\end{array}} \right.\)
Lưu ý: Ta có thế chọn điếm đi qua là \(B\) đế viết phương trình tham số hoặc có thế viết phương trinh chính tắc của đường thằng AB
b) Mặt phẳng nằm ngang (\({\rm{O}}x{\rm{y}})\) có vectơ pháp tuyến là \(\vec k = (0;0;1)\).
Ta có \(\sin (AB,(Oxy)) = \frac{{|0 - 0 + 7,5 \cdot 0 + ( - 0,4) \cdot 1|}}{{\sqrt {{0^2} + {{(7,5)}^2} + {{( - 0,4)}^2}} \cdot \sqrt {{0^2} + {0^2} + {1^2}} }} \approx 0,053\).
Suy ra . Vậy góc trượt nằm trong phạm vi cho phép.
c) Ta có \(\overrightarrow {MN} = ( - 5; - 5;0),\overrightarrow {MP} = ( - 5;0;0,5)\).
Xét vectơ \(\quad \vec n = [\overrightarrow {MN} ,\overrightarrow {MP} ] = \left( {\left| {\begin{array}{*{20}{c}}{ - 5}&0\\0&{0,5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - 5}\\{0,5}&{ - 5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 5}&{ - 5}\\{ - 5}&0\end{array}} \right|} \right)\), hay \(\vec n = ( - 2,5;2,5; - 25)\)
Khi đó \(\vec n\) là một vectơ pháp tuyến của mặt phẳng (MNP) hay chính là mặt phắng (a).
Phương trình mặt phắng (a) là: \( - 2,5(x - 5) + 2,5(y - 0) - 25(z - 0) = 0 \Leftrightarrow x - y + 10z - 5 = 0.\)
Vi C là vị trí mà máy bay xuyên qua đám mây đế hạ cánh nên C là giao điếm của đường thẳng AB và mặt phắng \((a)\).
Vi \(C \in AB\) nên gọi tọa độ điếm C là \({\rm{C}}(3,5; - 2 + 7,5{\rm{t}};0,4 - 0,4{\rm{t}})\).
Lại có \(C \in ({\rm{a}})\) nên ta có \(3,5 - ( - 2 + 7,5{\rm{t}}) + 10(0,4 - 0,4{\rm{t}}) - 5 = 0\), suy ra \({\rm{t}} = \frac{9}{{23}}\).
Vậy \( \subset \left( {3,5;\frac{{43}}{{46}};\frac{{28}}{{115}}} \right)\).
d) Vi \(D \in AB\) nên gọi tọa độ điếm \(D\) là \(D(3,5; - 2 + 7,5t;0,4 - 0,4t)\).
D là vị trí mà máy bay ở độ cao 120 m , tức là khoảng cách từ D đến mặt phẳng (Oxy) bẳng 120 m và bằng \(0,12\;{\rm{km}}\).
Ta có \({\rm{d}}({\rm{D}},({\rm{Oxy}})) = \frac{{\left| {0,4 - 0,4{t^\prime }} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = \left| {0,4 - 0,4{t^\prime }} \right|\).
Khi đó, \(\left| {0,4 - 0,4{{\rm{t}}^\prime }} \right| = 0,12 \Rightarrow \left[ {\begin{array}{*{20}{l}}{0,4 - 0,4{t^\prime } = 0,12}\\{0,4 - 0,4{t^\prime } = - 0,12}\end{array} \Rightarrow \left[ {\begin{array}{*{20}{l}}{{t^\prime } = 0,7}\\{{t^\prime } = 1,3}\end{array}} \right.} \right.\).
Với t' \( = 0,7\), ta có \(D(3,5;3,25;0,12)\).
Với t' \( = 1,3\), ta có \(D(3,5;7,75; - 0,12)\).
Vi D là vị trí độ cao của máy bay nên ta chọn $D(3,5 ; 3,25 ; 0,12)$.
e) Ta có \(DE = \sqrt {{{(3,5 - 3,5)}^2} + {{(4,5 - 3,25)}^2} + {{(0 - 0,12)}^2}} \approx 1,256(\;{\rm{km}})\)
Vì tầm nhìn xa của phi công sau khi ra khỏi đám mây là \(900\;{\rm{m}} = 0,9\;{\rm{km}} < 1,256\;{\rm{km}}\) nên người phi công đó không đạt được quy định an toàn bay.
Lời giải
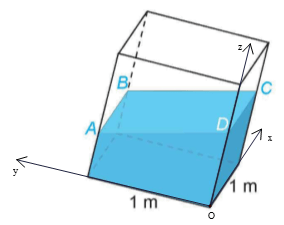
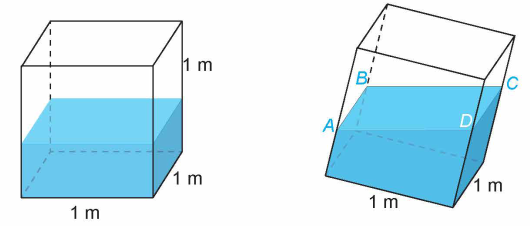
a) Chọn hệ trục tọa độ như hình vẽ.
\(40\;{\rm{cm}} = 0,4\;{\rm{m}},44\;{\rm{cm}} = 0,44\;{\rm{m}},48\;{\rm{cm}} = 0,48\;{\rm{m}}{\rm{. }}\)
Khi đó ta có \({\rm{A}}(0;1;0,4),{\rm{B}}(1;1;0,44),{\rm{C}}(1;0;0,48)\).
Có \(\overrightarrow {AB} = (1;0;0,04)\). Vi ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{1 - {x_D} = 1}\\{ - {y_D} = 0}\\{0,48 - {z_D} = 0,04}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_D} = 0}\\{{y_D} = 0}\\{{z_D} = 0,44}\end{array}} \right.\)
Suy ra \(D(0;0;0,44)\).
Vậy khoảng cách từ điểm \(D\) đến đáy bể là 44 cm .
b) Ta có đáy bể nằm trong mặt phẳng \({\rm{Oxy}}:z = 0\) có vectơ pháp tuyến \(\vec k = (0;0;1)\)
Ta có \(\quad \overrightarrow {AB} = (1;0;0,04),\quad \overrightarrow {AC} = (1; - 1;0,08)\), \([\overrightarrow {AB} ,\overrightarrow {AC} ] = (0,04; - 0,04; - 1)\)
Mặt phẳng \((ABCD)\) đi qua \({\rm{A}}(0;1;0,4)\) và có vectơ pháp tuyến \(\vec n = [\overrightarrow {AB} ,\overrightarrow {AC} ] = (0,04; - 0,04; - 1)\) có phương trình là: \(0,04x - 0,04(y - 1) - (z - 0,4) = 0 \Leftrightarrow 0,04x - 0,04y - z + 0,44 = 0.{\rm{ }}\)
Do đó góc giữa đáy bể và mặt phẳng nằm ngang chính là góc giữa mặt phẳng (ABCD) và mặt đáy.
\({\rm{ C\'o }}\cos ((ABCD),(Oxy)) = \frac{{| - 1|}}{{\sqrt 1 \cdot \sqrt {{{0,04}^2} + {{( - 0,04)}^2} + {{( - 1)}^2}} }} = \frac{{25}}{{\sqrt {627} }}\). Suy raLời giải
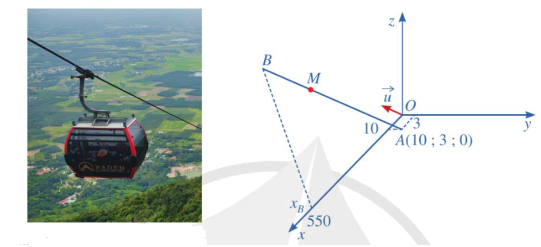
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
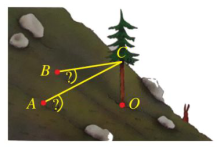
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.