Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hinh hoá bằng hàm số \(P\left( t \right) = \frac{a}{{b + {e^{ - 0,75t}}}}\), trong đó thời gian \(t\) được tính bằng giờ. Tại thời điểm ban đầu \(t = 0\), quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Tìm các giá trị của \(a\) và \(b\). Theo mô hình này, điều gì xảy ra với quần thể nấm men về lâu dài?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: \(P'\left( t \right) = \frac{{0,75a{{\rm{e}}^{ - 0,75t}}}}{{{{\left( {b + {{\rm{e}}^{ - 0,75t}}} \right)}^2}}},t \ge 0\).
Theo đề bài, ta có: \(P\left( 0 \right) = 20\) và \(P'\left( 0 \right) = 12\).
Do đó, ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{\frac{a}{{b + 1}} = 20}\\{\frac{{0,75a}}{{{{\left( {b + 1} \right)}^2}}} = 12}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 20\left( {b + 1} \right)}\\{\frac{{15}}{{b + 1}} = 12.}\end{array}} \right.} \right.\)
Giải hệ phương trình này, ta được \(a = 25\) và \(b = \frac{1}{4}\).
Khi đó, \(P'\left( t \right) = \frac{{18,75{{\rm{e}}^{ - 0,75t}}}}{{{{\left( {\frac{1}{4} + {{\rm{e}}^{ - 0,75t}}} \right)}^2}}} > 0,\forall t \ge 0\), tức là số lượng quần thể nấm men luôn tăng.
Tuy nhiên, do \(\mathop {\lim }\limits_{t \to + \infty } P\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{25}}{{\frac{1}{4} + {{\rm{e}}^{ - 0.75t}}}} = 100\) nên số lượng quần thể nấm men tăng nhưng không vượt quá 100 tế bào.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hàm số \(y = C\left( x \right) = \frac{{300x}}{{100 - x}},0 \le x < 100\).
Ta có:\(y' = \frac{{30000}}{{{{\left( {100 - x} \right)}^2}}} > 0\), với mọi \(x \in [0;100)\). Do đó hàm số luôn đồng biến trên nửa khoảng \(\left[ {0;100} \right)\) và\(\mathop {\lim }\limits_{x \to {{100}^ - }} C\left( x \right) = \mathop {\lim }\limits_{x \to {{100}^ - }} \frac{{300x}}{{100 - x}} = + \infty \) nên đồ thị hàm số có tiệm cận đứng là \(x = 100\).
Bảng biến thiên:
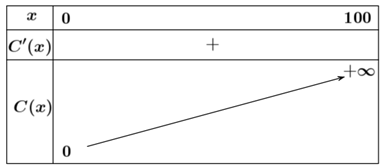
a) Chi phí cần bỏ ra \(C\left( x \right)\) sẽ luôn tăng khi \(x\) tăng.
b) Vì \(\mathop {\lim }\limits_{x \to {{100}^ - }} C\left( x \right) = + \infty \) (hàm số \(C\left( x \right)\) không xác định khi \(x = 100)\) nên nhà máy không thể loại bỏ \(100\% \) chất gây ô nhiễm không khí (dù bỏ ra chi phí là bao nhiêu đi chăng nữa).
Lời giải
a) Hàm chi phí biên là \(C'\left( x \right) = 300 - 5x + 0,375{x^2}\).
b) Ta có: \(C'\left( {200} \right) = 300 - 5 \cdot 200 + 0,375 \cdot {200^2} = 14300\).
Chi phí biên tại \(x = 200\) là 14300 nghìn đồng, nghĩa là chi phí để sản xuất thêm một đơn vị hàng hoá tiếp theo (đơn vị hàng hoá thứ 201) là khoảng 14300 nghìn đồng.
c) Chi phí sản xuất đơn vị hàng hoá thứ 201 là
\(C\left( {201} \right) - C\left( {200} \right) = 1004372,625 - 990000 = 14372,625{\rm{ }}\)(nghìn đồng)
Giá trị này xấp xỉ với chi phí biên \(C'\left( {200} \right)\) đã tính ở câu trên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo