Câu hỏi:
19/03/2025 40Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \[y = \frac{{mx - 8}}{{x + 2}}\] có hai đường tiệm cận.
Đáp án chính xác
Sách mới 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 49k/cuốn).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Với m = −4 thì \[y = \frac{{ - 4x - 8}}{{x + 2}} = - 4\] không thỏa mãn.
Do đó m ≠ −4 thì hàm số luôn có hai đường tiệm cận x = −2; y = m.
Nhà sách VIETJACK:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm tất cả giá trị của tham số m để đường tiệm cận xiên của đồ thị hàm số \(y = 2mx + 3 - \frac{4}{{x + 1}}\) đi qua điểm M(1; 7).
Xem đáp án »
19/03/2025
87
Câu 2:
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số \(y = \frac{{{x^2} + m}}{{{x^2} - 3x + 2}}\) có đúng hai đường tiệm cận.
Xem đáp án »
19/03/2025
79
Câu 3:
Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - 8x + m}}\] có 3 đường tiệm cận?
Xem đáp án »
19/03/2025
67
Câu 4:
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ. Định tham số m để giao điểm của đường tiệm cận đứng và tiệm cận ngang là điểm I(−1; 1).
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ. Định tham số m để giao điểm của đường tiệm cận đứng và tiệm cận ngang là điểm I(−1; 1).
Xem đáp án »
19/03/2025
63
Câu 5:
Cho hàm số y = f(x) có bảng biến thiên:
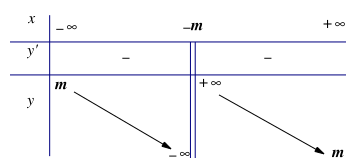
![Cho hàm số y = f(x) có bảng biến thiên: Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để hàm số có 4 tiệm cận? (ảnh 1)](https://video.vietjack.com/upload2/images/1742397066/1742397854-image3.png)
Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để hàm số có 4 tiệm cận?
Cho hàm số y = f(x) có bảng biến thiên:
Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để hàm số có 4 tiệm cận?
Xem đáp án »
19/03/2025
52
Câu 6:
Biết rằng đồ thị của hàm số \(y = \frac{{\left( {n - 3} \right)x + n - 2017}}{{x + m + 3}}\) (m, n là các số thực) nhận trục hoành làm tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng m + n.
Xem đáp án »
19/03/2025
46
Câu 7:
Cho hàm số y = f(x) có bảng biến thiên sau:
Tìm tổng số các giá trị nguyên dương của tham số m ∈ (−10; 10) để đồ thị hàm số y = f(x) có tổng số đường tiệm cận đứng và đường tiệm cận ngang là 4.
Cho hàm số y = f(x) có bảng biến thiên sau:
Tìm tổng số các giá trị nguyên dương của tham số m ∈ (−10; 10) để đồ thị hàm số y = f(x) có tổng số đường tiệm cận đứng và đường tiệm cận ngang là 4.
Xem đáp án »
19/03/2025
45
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận