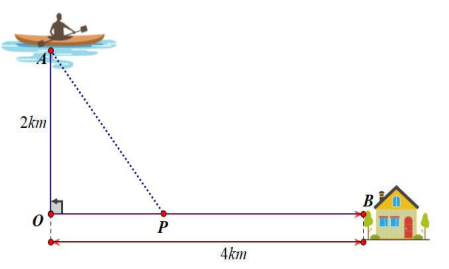
Một loại vi khuẩn được tiêm một loại thuốc kích thích sự sinh sản. Sau t phút, số vi khuẩn được xác định theo công thức N(t) = 1000 + 30t2 – t3 (0 ≤ t ≤ 30). Hỏi sau bao giây thì số vi khuẩn lớn nhất?
A. 20;
B. 10;
C. 1200;
D. 1100.
Quảng cáo
Trả lời:
Đáp án đúng là: A
Xét hàm số N(t) = 1000 + 30t2 – t3 (0 t 30).
Có N'(t) = 60t – 3t2; N'(t) = 0 t = 0 hoặc t = 20.
Ta có bảng biến thiên
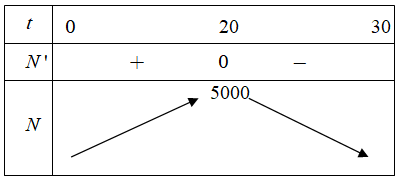
Với t = 20 giây thì số vi khuẩn lớn nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 40
phút;
B. 44 phút;
C. 30 phút;
D. 38 phút.
Lời giải
Đáp án đúng là: A
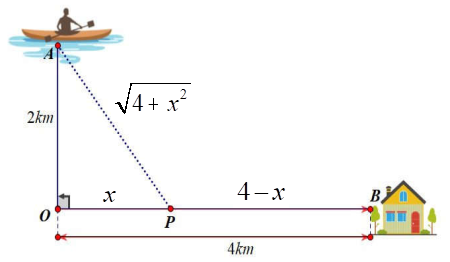
Đặt OP = x (0 < x < 4) BP = 4 – x; \(AP = \sqrt {4 + {x^2}} \).
Khoảng thời gian để anh Ba từ vị trí xuất phát đến được điểm B là:
\({t_{\left( x \right)}} = {t_{AP}} + {t_{PB}} = \frac{{\sqrt {4 + {x^2}} }}{6} + \frac{{4 - x}}{{10}}\,\,\left( h \right)\, \Rightarrow {t'_{\left( x \right)}} = \frac{x}{{6\sqrt {4 + {x^2}} }} - \frac{1}{{10}}\).
\({t'_{\left( x \right)}} = 0 \Leftrightarrow \frac{x}{{6\sqrt {4 + {x^2}} }} - \frac{1}{{10}} = 0 \Leftrightarrow 3\sqrt {4 + {x^2}} = 5x \Leftrightarrow \left\{ \begin{array}{l}0 < x < 4\\4{x^2} = 9\end{array} \right. \Leftrightarrow x = \frac{3}{2}.\)
Bảng biến thiên
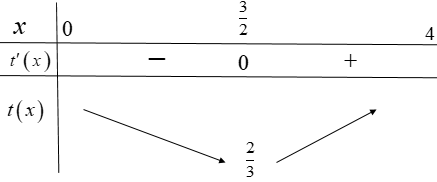
Từ bảng biến thiên suy ra khoảng thời gian ngắn nhất để anh Ba từ vị trí xuất phát đến được điểm B là: \({t_{\min }} = \frac{2}{3}\,\left( h \right)\, = \frac{2}{3}.60\,\left( {ph\'u t} \right) = 40\,ph\'u t.\)
</></>
Câu 2
A. 1418000 đồng.
B. 1403000 đồng.
C. 1402000 đồng.
D. 1417000 đồng.
Lời giải
Đáp án đúng là: C
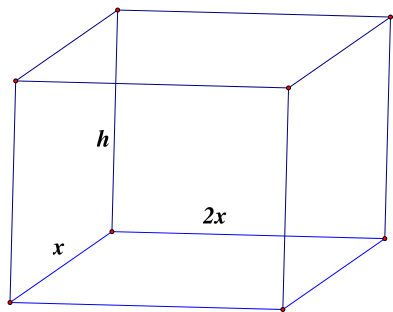
Gọi x là chiều rộng của đáy thùng, x > 0, đơn vị m.
chiều dài của đáy thùng là: 2x.
Ta có V = x.2x.h = 10 \(h = \frac{5}{{{x^2}}}\).
Chi phí làm đáy thùng là: 2x2.75 = 150x2 (đơn vị nghìn đồng).
Chi phí làm diện tích xung quanh là : \(\left( {2x.\frac{5}{{{x^2}}} + 2.2x.\frac{5}{{{x^2}}}} \right).55 = \frac{{1650}}{x}\) (đơn vị nghìn đồng).
Chi phí làm thùng là : \(T = 150{x^2} + \frac{{1650}}{x}\) (đơn vị nghìn đồng).
Xét hàm số \(T = 150{x^2} + \frac{{1650}}{x}\), với x > 0.
Ta có \(T'\left( x \right) = 300x - \frac{{1650}}{{{x^2}}}\) ; \(T'\left( x \right) = 0 \Leftrightarrow x = \sqrt[3]{{\frac{{11}}{2}}}\).
Bảng biến thiên
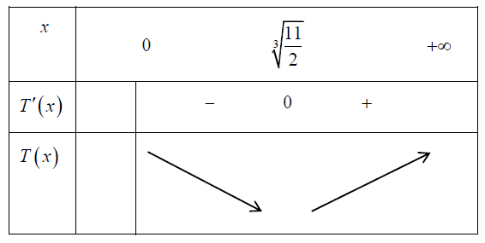
Dựa vào bảng biến thiên T(x) đạt giá trị nhỏ nhất tại \(x = \sqrt[3]{{\frac{{11}}{2}}}\).
Vậy chi phí ít nhất bằng \(T = 150{\left( {\sqrt[3]{{\frac{{11}}{2}}}} \right)^2} + \frac{{1650}}{{\sqrt[3]{{\frac{{11}}{2}}}}} \approx 1402000\) đồng.
Câu 3
A. 289 m/s.
B. 105 m/s.
C. 111 m/s.
D. 487 m/s.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Ngay từ lúc bắt đầu sử dụng độc tố;
B. Sau 0,5 giờ;
C. Sau 2 giờ;
D. Sau 1 giờ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Dân số của quốc gia vào năm 2030 là: 108,763 (triệu người);
B. Dân số của quốc gia vào năm 2035 là: 125,488 (triệu người);
C. Xem N(t) là hàm số của biến số t xác định trên đoạn [0; 50]. Khi đó hàm số N(t) đồng biến trên đoạn [0; 50];
D. Đạo hàm của hàm số N(t) biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/năm). Vậy vào năm 2046 thì tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/ năm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.