Phần III. Trắc nghiệm trả lời ngắn
(Gồm 5 câu hỏi, hãy viết câu trả lời/đáp án vào bài làm mà không cần trình bày lời giải chi tiết)
Một hình chóp tam giác đều có thể tích là \({V_1}.\) Nếu tăng chiều cao của hình chóp đó lên 3 lần và giữ nguyên độ dài cạnh của tam giác đáy thì được một hình chóp mới có thể tích là \({V_2}.\) Tính \(\frac{{{V_2}}}{{{V_1}}}.\)
Phần III. Trắc nghiệm trả lời ngắn
(Gồm 5 câu hỏi, hãy viết câu trả lời/đáp án vào bài làm mà không cần trình bày lời giải chi tiết)
Một hình chóp tam giác đều có thể tích là \({V_1}.\) Nếu tăng chiều cao của hình chóp đó lên 3 lần và giữ nguyên độ dài cạnh của tam giác đáy thì được một hình chóp mới có thể tích là \({V_2}.\) Tính \(\frac{{{V_2}}}{{{V_1}}}.\)
Quảng cáo
Trả lời:
Đáp án: 3
Gọi chiều cao và diện tích đáy của hình chóp tam giác đều ban đầu lần lượt là \({h_1}\) và \({S_1}.\)
Khi tăng chiều cao của hình chóp đó lên 3 lần thì chiều cao của hình chóp mới là \(2{h_1}.\)
Thể tích hình chóp tam giác ban đầu là: \({V_1} = \frac{1}{3} \cdot {S_1} \cdot {h_1}.\)
Thể tích hình chóp tam giác mới là: \({V_2} = \frac{1}{3} \cdot {S_1} \cdot 3{h_1}.\)
Ta có: \(\frac{{{V_2}}}{{{V_1}}} = \frac{{\frac{1}{3} \cdot {S_1} \cdot 3{h_1}}}{{\frac{1}{3} \cdot {S_1} \cdot {h_1}}} = 3.\) Vậy \(\frac{{{V_2}}}{{{V_1}}} = 3.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng.
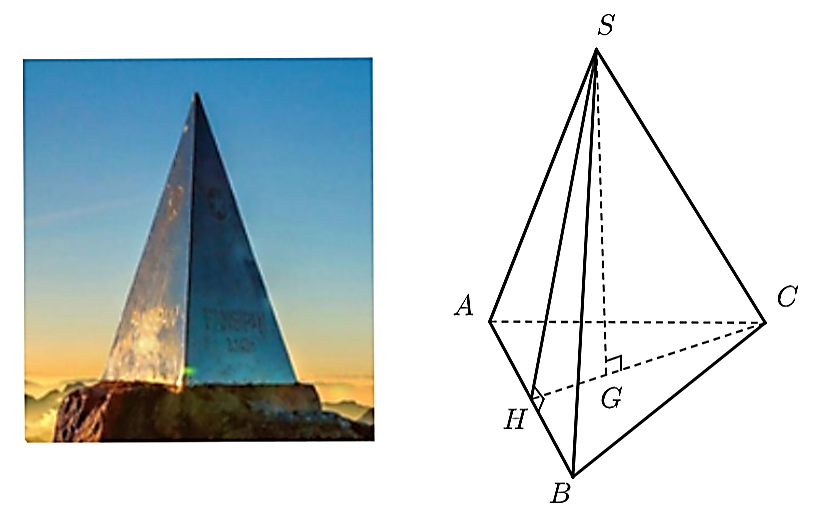
Mặt đáy của hình chóp \(S.ABC\) là một tam giác đều \(ABC\) có cạnh \(60{\rm{ cm}}{\rm{.}}\) Gọi đường cao của mặt đáy là \(CH\), ta có \(CH\) đồng thời là đường trung tuyến.
\(HA = HB = \frac{{AB}}{2} = 30{\rm{ cm}}{\rm{.}}\)
b) Đúng.
Xét tam giác \(BHC\) vuông tại \(H\). Theo định lý Pythagore ta có: \(C{B^2} = H{B^2} + H{C^2}\) hay \({60^2} = {30^2} + H{C^2}\) suy ra \(C{H^2} = {60^2} - {30^2} = 2{\rm{ }}700\) nên \(CH = \sqrt {2700} = 30\sqrt 3 {\rm{ }}\left( {{\rm{cm}}} \right)\).
c) Sai.
Vì \(G\) là trọng tâm của mặt đáy nên \(GH = \frac{1}{3}HC = \frac{{30\sqrt 3 }}{3} = 10\sqrt 3 {\rm{ }}\left( {{\rm{cm}}} \right)\).
Hình chóp \(S.ABC\) có đường cao \(SG\) nên \(SG \bot HC.\)
Xét tam giác \(SHG\) vuông tại \(G\). Theo định lý Pythagore, ta có:
\(S{H^2} = S{G^2} + H{G^2}\)
\(S{H^2} = {90^2} + {30^2} = 9000\)
Suy ra \(SH = \sqrt {9000} = 30\sqrt {10} {\rm{ cm}}{\rm{.}}\)
d) Đúng.
Vậy diện tích xung quanh của hình chóp là \(S = 3 \cdot \frac{1}{2} \cdot 60 \cdot 30\sqrt {10} \approx 8538{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Lời giải
a) Đúng.
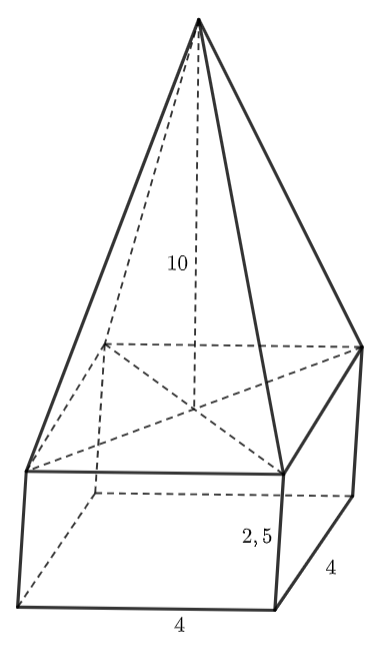
Phần dưới của khối bê tông có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh \(4{\rm{ dm,}}\) chiều cao \({\rm{2,5 dm}}{\rm{.}}\)
Do đó, thể tích của khối bê tông này là: \({V_1} = S.h = {4^2}.2,5 = 40{\rm{ }}\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right)\)
b) Đúng.
Phần trên của khối bê tông có dạng hình chóp tứ giác đều có độ dài cạnh của mặt đáy là \(4{\rm{ dm,}}\) chiều cao là \({\rm{10 dm}}{\rm{.}}\)
Do đóm thể tích của khối bê tông hình chóp này là: \({V_2} = \frac{1}{3}S.h = \frac{1}{3}{.4^2}.10 = \frac{{160}}{3}{\rm{ }}\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right)\).
c) Đúng.
Tỉ lệ thể tích khối bê tông dạng hình hộp chữ nhật so với khối bê tông hình chóp là
\(40:\frac{{160}}{3} = \frac{3}{4}\).
d) Sai.
Vậy thể tích của khối bê tông trên gồm hai khối là khối hình hộp chữ nhật và khối hình chóp tứ giác đều.
Vậy thể tích của khối bê tông này là: \(40 + \frac{{160}}{3} = \frac{{280}}{3} \approx 93,3{\rm{ }}\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.