Một sinh viên sau khi ra trường và xin vào làm cho một trung tâm với mức lương khởi điểm là \[100\] triệu đồng một năm. Cứ sau mỗi năm, trung tâm trả thêm cho sinh viên \[20\] triệu đồng. Gọi \[{u_n}\] (triệu đồng) là số tiền lương mà sinh viên đó nhận được ở năm thứ \[n\]. Xét tính đúng sai của các khẳng định sau:
a) Số tiền lương sinh viên nhận được ở năm thứ hai là \[120\] triệu đồng.
b) Số tiền lương sinh viên nhận được ở năm thứ 10 là \[300\] triệu đồng.
c) Tiền lương sau mỗi năm của sinh viên đó là cấp số cộng có \[{u_1} = 120\] và công sai \[d = 20\].
d) Giả sử, mỗi năm bạn sinh viên chi tiêu tiết kiệm \[70\] triệu đồng. Vậy sau ít nhất \[12\] năm thì sinh viên đó mua được căn chung cư \[2\] tỉ đồng.
Một sinh viên sau khi ra trường và xin vào làm cho một trung tâm với mức lương khởi điểm là \[100\] triệu đồng một năm. Cứ sau mỗi năm, trung tâm trả thêm cho sinh viên \[20\] triệu đồng. Gọi \[{u_n}\] (triệu đồng) là số tiền lương mà sinh viên đó nhận được ở năm thứ \[n\]. Xét tính đúng sai của các khẳng định sau:
a) Số tiền lương sinh viên nhận được ở năm thứ hai là \[120\] triệu đồng.
b) Số tiền lương sinh viên nhận được ở năm thứ 10 là \[300\] triệu đồng.
c) Tiền lương sau mỗi năm của sinh viên đó là cấp số cộng có \[{u_1} = 120\] và công sai \[d = 20\].
d) Giả sử, mỗi năm bạn sinh viên chi tiêu tiết kiệm \[70\] triệu đồng. Vậy sau ít nhất \[12\] năm thì sinh viên đó mua được căn chung cư \[2\] tỉ đồng.
Quảng cáo
Trả lời:
Hướng dẫn giải
|
a) Đ |
b) S |
c) S |
d) S |
Ta thấy, số tiền lương năm sau hơn năm trước \[20\] triệu đồng nên \[\left( {{u_n}} \right)\] là cấp số cộng có \[{u_1} = 100\] và công sai \[d = 20\].
Do đó, \[{u_n} = {u_1} + \left( {n - 1} \right)d = 100 + \left( {n - 1} \right).20 = 20n + 80\].
Số tiền lương sinh viên nhận được ở năm thứ hai là \[{u_2} = 100 + \left( {2 - 1} \right).20 = 120\] (triệu đồng).
Số tiền lương sinh viên nhận được ở năm thứ 10 là \[{u_{10}} = 100 + \left( {10 - 1} \right).20 = 280\] (triệu đồng).
Số tiền bạn sinh viên tiết kiệm được sau \[n\] năm là
\[S = \frac{n}{2}\left[ {2{u_1} + \left( {n - 1} \right)d} \right] - 70n\]
\[ = \frac{n}{2}\left[ {2.100 + \left( {n - 1} \right).20} \right] - 70n\]
\[ = 10{n^2} + 20n\] (triệu đồng).
Ta có: \[S \ge 2000 \Leftrightarrow 10{n^2} + 20n \ge 2000\]
\[ \Leftrightarrow 10{n^2} + 20n - 2000 \ge 0 \Leftrightarrow \left[ \begin{array}{l}n \ge 13,1{\rm{ }}\left( {TM} \right)\\n \le - 15,1{\rm{ }}\left( L \right)\end{array} \right.\].
Do đó, sau ít nhất 14 năm thì sinh viên có thể mua được chung cư 2 tỉ đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
|
a) Đ |
b) S |
c) Đ |
d) Đ |
![Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình c (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/31-1760833938.png)
a) Ta có: \[\left\{ \begin{array}{l}S \in \left( {SAB} \right) \cap \left( {SCD} \right)\\AB\parallel CD\end{array} \right.\].
Suy ra giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\] là đường thẳng qua \[S\] và song song với \[AB\].
b) Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\).
Ta có \[\left\{ \begin{array}{l}O \in \left( {SAC} \right) \cap \left( {SBD} \right)\\S \in \left( {SAC} \right) \cap \left( {SBD} \right)\end{array} \right. \Rightarrow SO = \left( {SAC} \right) \cap \left( {SBD} \right)\].
Suy ra giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right)\] là đường thẳng \[SO.\]
c) Ta có: \[\left\{ \begin{array}{l}G \in \left( {SAB} \right) \cap \left( {JIG} \right)\\AB\parallel JI\end{array} \right.\]
Suy ra giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {IGJ} \right)\] là đường thẳng qua \[G\] và song song với \[AB\].
Lại có \(AB||CD\) nên giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {IGJ} \right)\] là đường thẳng qua \[G\] và song song với \[CD\].
d) Theo đề, ta có: \[NA = \frac{1}{3}SA \Rightarrow SN = \frac{2}{3}SA \Rightarrow \frac{{SN}}{{SA}} = \frac{2}{3}.\]
Lại có: \[SM = \frac{2}{3}SD \Leftrightarrow \frac{{SM}}{{SD}} = \frac{2}{3}\] nên \[\frac{{SN}}{{SA}} = \frac{{SM}}{{SD}} = \frac{2}{3}\]. Suy ra \[MN\parallel AD\].
Ta có: \[\left\{ \begin{array}{l}G \in \left( {GBC} \right) \cap \left( {GMN} \right)\\MN\parallel AD\\BC\parallel AD\end{array} \right.\]
Suy ra giao tuyến của hai mặt phẳng \[\left( {GMN} \right)\] và \[\left( {GBC} \right)\] là đường thẳng qua \[G\] và song song với \[AD.\]
Lời giải
Hướng dẫn giải
|
a) Đ |
b) S |
c) Đ |
d) S |
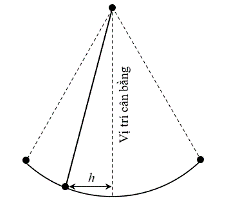
Ta có: \[h = \left| x \right| = \left| {1,5\cos \left( {\frac{{\pi t}}{4}} \right)} \right| \le 1,5.\]
a) Vật ở xa vị trí cân bằng nhất nghĩa là \[h = 1,5{\rm{ m}}\].
Khi đó \[\cos \left( {\frac{{\pi t}}{4}} \right) = \pm 1\]\[ \Leftrightarrow \left[ \begin{array}{l}\frac{{t\pi }}{4} = k2\pi \\\frac{{t\pi }}{4} = \pi + k2\pi \end{array} \right.{\rm{ }}\left( {k \in \mathbb{Z}} \right)\] \[ \Leftrightarrow \left[ \begin{array}{l}t = 8k\\t = 4 + 8k\end{array} \right.,{\rm{ }}\left( {k \in \mathbb{Z}} \right)\].
b) Trong 10 giây đầu tiên thì vật ở xa vị trí cân bằng nhất tại các thời điểm \[t = 0;\]
\[t = 4;t = 8\] giây.
c) Khi vật ở vị trí cân bằng thì \[x = 0 \Leftrightarrow 1,5\cos \left( {\frac{{\pi t}}{4}} \right) = 0\]\[ \Leftrightarrow \cos \left( {\frac{{\pi t}}{4}} \right) = 0\]
\[ \Leftrightarrow \frac{{\pi t}}{4} = \frac{\pi }{2} + k\pi ,{\rm{ }}\left( {k \in \mathbb{Z}} \right) \Leftrightarrow t = 2 + 4k\left( {k \in \mathbb{Z}} \right)\].
d) Ta có: \[0 < t < 20 \Leftrightarrow 0 < 2 + 4k < 20\]\[ \Leftrightarrow - \frac{1}{2} < k < \frac{{18}}{4}\].
Mà \[k \in \mathbb{Z}\] nên \[k \in \left\{ {0;1;2;3;4} \right\}\].
Suy ra \[t \in \left\{ {2;6;10;14;18} \right\}.\]
Vậy trong khoảng thời gian từ 0 đến 20 giây thì vật ở vị trí cân bằng tại các thời điểm \[t = 2;{\rm{ }}t = 6;{\rm{ }}t = 10;{\rm{ }}t = 14;{\rm{ }}t = 18\] giây; tức là có 5 lần vật qua vị trí cân bằng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.