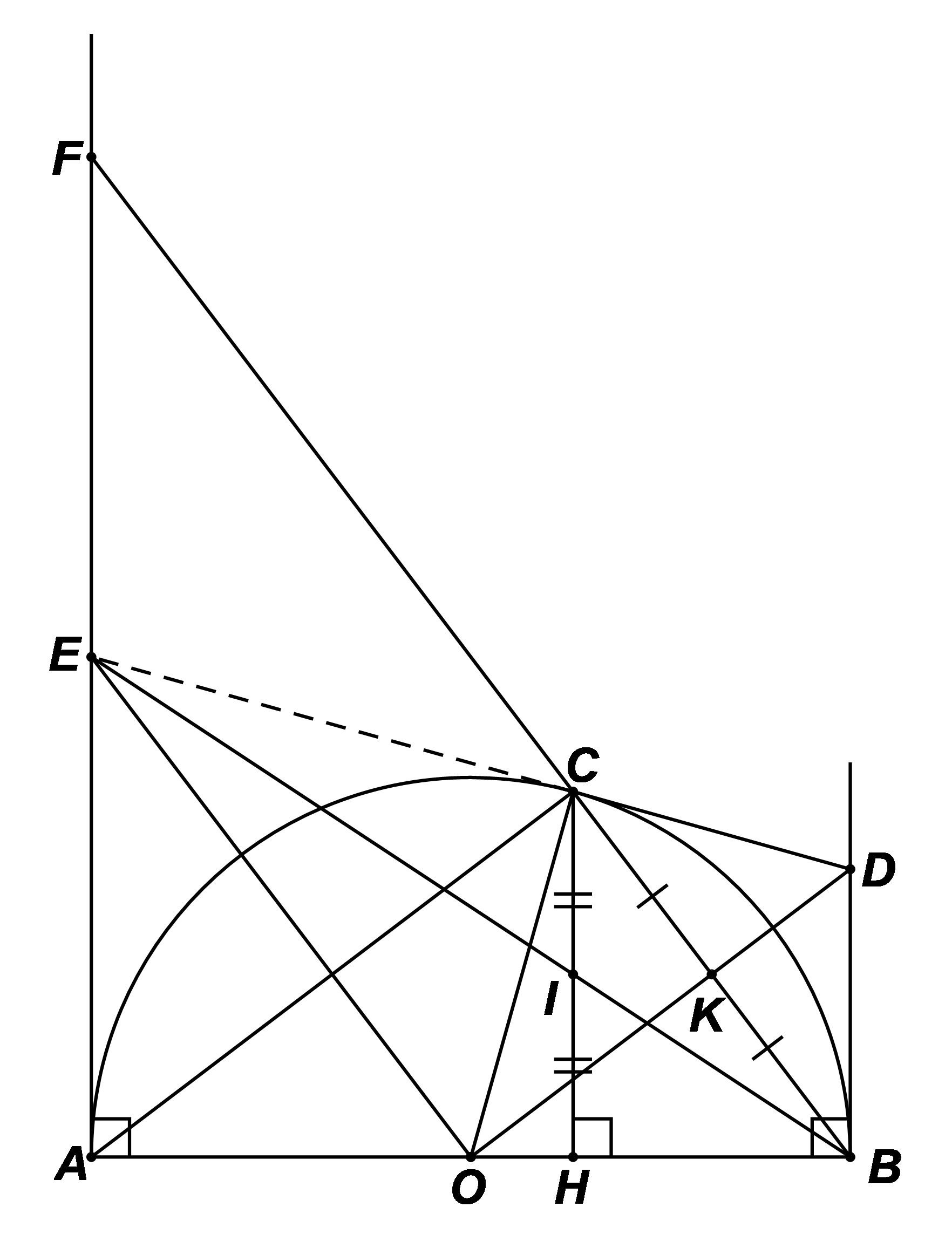(0,5 điểm) Một khu đất có dạng nửa hình tròn với bán kính là \[14{\rm{ m}}{\rm{.}}\] Người ta muốn xây dựng một khu vui chơi hình chữ nhật ở bên trong nửa đường tròn đó như hình vẽ, biết rằng một cạnh của hình chữ nhật nằm dọc trên đường kính của nửa đường tròn. Tính diện tích lớn nhất của khu vui chơi có thể xây dựng.
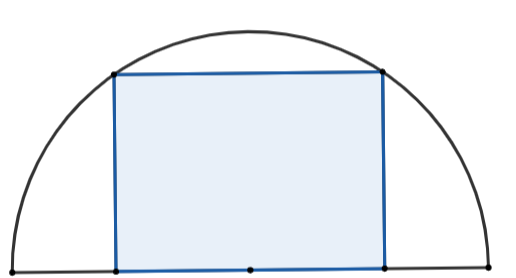
(0,5 điểm) Một khu đất có dạng nửa hình tròn với bán kính là \[14{\rm{ m}}{\rm{.}}\] Người ta muốn xây dựng một khu vui chơi hình chữ nhật ở bên trong nửa đường tròn đó như hình vẽ, biết rằng một cạnh của hình chữ nhật nằm dọc trên đường kính của nửa đường tròn. Tính diện tích lớn nhất của khu vui chơi có thể xây dựng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Gọi các điểm như hình vẽ dưới đây:
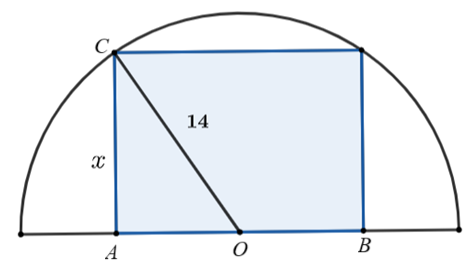
Gọi \[x\] là độ dài cạnh \(AC\) hình chữ nhật không nằm dọc theo đường kính đường tròn \[\left( {0 < x < 14} \right)\].
Khi đó, ta tính được độ dài cạnh của hình chữ nhật nằm dọc trên đường tròn là:
\[AB = 2AO = 2\sqrt {O{C^2} - A{C^2}} = 2\sqrt {{{14}^2} - {x^2}} {\rm{ }}\left( {\rm{m}} \right)\].
Diện tích hình chữ nhật là \[S = 2x\sqrt {{{14}^2} - {x^2}} {\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right)\].
Ta có: \[{S^2} = 4{x^2}\left( {196 - {x^2}} \right) = - 4{x^4} + 2 \cdot 2{x^2} \cdot 196 - {196^2} + {196^2} = - {\left( {2{x^2} - 196} \right)^2} + {196^2}\] .
Nhận thấy \[ - {\left( {2{x^2} - 196} \right)^2} \le 0\], do đó \[ - {\left( {2{x^2} - 196} \right)^2} + {196^2} \le {196^2}\].
Suy ra \[{S^2} \le {196^2}\], nên \[S \le \sqrt {{{196}^2}} \] hay \[S \le 196{\rm{ }}{{\rm{m}}^2}\].
Dấu “=” xảy ra khi và chỉ khi \[ - {\left( {2{x^2} - 196} \right)^2} = 0\], hay \[2{x^2} - 196 = 0\], tức là \[x = 7\sqrt 2 {\rm{ }}\left( {\rm{m}} \right)\].
Vậy diện tích lớn nhất của khu vui chơi đó là \[196{\rm{ }}{{\rm{m}}^2}\].
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
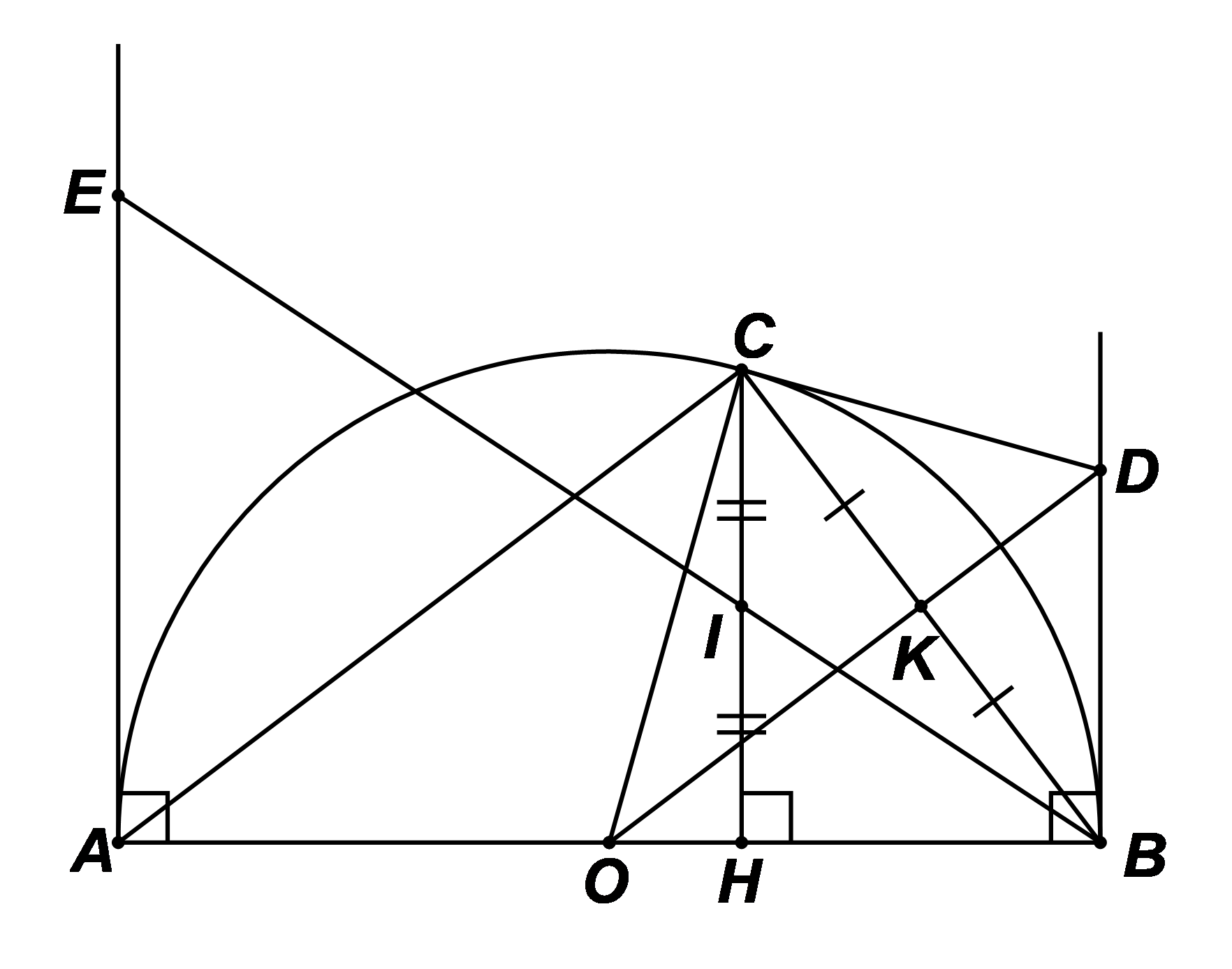
a) Xét \[\Delta OBC\] cân tại \[O\] (do \[OC = OB = R\]) nên đường trung tuyến \[OK\] cũng là đường cao của \[\Delta OBC.\] Suy ra \[OK \bot BC\] hay \[OD \bot BC\].
Xét nửa đường tròn \(\left( O \right)\) đường kính \(AB,\) có \[\widehat {ACB}\] là góc nội tiếp chắn nửa đường tròn nên \[\widehat {ACB} = 90^\circ .\]
Vậy \[\Delta ABC\] vuông tại \[C\].
b) Xét \[\Delta OBC\] cân tại \[O\] (do \[OC = OB = R\]) nên đường trung tuyến \[OK\] cũng là đường phân giác của \[\Delta OBC.\] Do đó \(\widehat {BOD} = \widehat {COD}.\)
Xét \[\Delta CDO\] và \[\Delta BDO\] có:
\[OD\] là cạnh chung; \(\widehat {BOD} = \widehat {COD}\); \[OB = OC\]
Do đó \[\Delta CDO = \Delta BDO\] (c.g.c).
Suy ra \[\widehat {DCO} = \widehat {DBO} = 90^\circ \] (hai góc tương ứng).
Như vậy, \[OC \bot DC\] tại \[C\] thuộc \(\left( O \right)\) hay \[DC\] là tiếp tuyến của đường tròn \[\left( O \right)\].
|
c) Gọi \[F\] là giao điểm của \[BC,\,\,AE.\] Ta có: \[IC \bot AB\] và \[AF \bot AB\], suy ra \[IC\,{\rm{//}}\,AF\] hay \[IC\,{\rm{//}}\,EF\]. Xét \[\Delta BEF\], có: \[\frac{{IC}}{{EF}} = \frac{{IB}}{{EB}}\] (Hệ quả định lí Thalès) (1) Xét \[\Delta BAE\], có: \[\frac{{IH}}{{AE}} = \frac{{IB}}{{EB}}\] (Hệ quả định lí Thalès) (2) Từ (1) và (2) suy ra \[\frac{{IC}}{{EF}} = \frac{{IH}}{{EA}}\], mà \[IC = IH\] (do \(I\) là trung điểm của \(CH)\) nên \[EF = EA\] hay \[E\] là trung điểm của \[AF.\] Ta có \[\widehat {FCA} = 90^\circ \] (cùng bù với \[\widehat {ACB} = 90^\circ \]) nên \[\Delta FCA\] vuông tại \[C\].
Xét \(\Delta ACF\) vuông tại \(C,\) có \(CE\) là đường trung tuyến ứng với cạnh huyền \(AF\) nên \[CE = EA = EF = \frac{1}{2}AF.\] Xét \[\Delta CEO\] và \[\Delta AEO\], có: \[CE = AE\], \[OC = OA\] và \[OE\] là cạnh chung Do đó \[\Delta CEO = \Delta AEO\] (c.c.c) Suy ra \[\widehat {ECO} = \widehat {EAO} = 90^\circ \] (hai góc tương ứng). Ta có: \[\widehat {ECO} + \widehat {OCD} = 90^\circ + 90^\circ = 180^\circ \] hay \[\widehat {ECD} = 180^\circ \]. Vậy ba điểm \[E,C,D\] thẳng hàng. |
|
Câu 2
A. \(x \ne 0;\,\,x \ne 1.\)
B. \(x \ne 0;\,\,x \ne - 1.\)
C. \(x \ne 3;\,\,x \ne 2.\)
D. \(x \ne 0.\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Điều kiện xác định của phương trình \(\frac{{x + 3}}{{x + 1}} + \frac{{x - 2}}{x} = 2\) là \(x + 1 \ne 0\) và \(x \ne 0\) hay \(x \ne - 1;\,\,x \ne 0.\)
Câu 3
A. \(\left\{ \begin{array}{l}3x - y = 5\\x + 2y = - 1\end{array} \right..\)
B. \(\left\{ \begin{array}{l} - 3y = 6\\3x + 5y = 15\end{array} \right..\)
C. \(\left\{ \begin{array}{l}{x^2} - 4{y^2} = 0\\2x + 5y = 7\end{array} \right..\)
D. \(\left\{ \begin{array}{l}2x - 3y = - 3\\2x + 5y = 7\end{array} \right..\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \({\left( { - \sqrt 5 } \right)^2}.\)
B. \(\sqrt {{5^2}} .\)
C. \(\sqrt {{{\left( { - 5} \right)}^2}} .\)
D. \( - {\left( {\sqrt 5 } \right)^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 1.
B. 2.
C. 3.
D. 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo