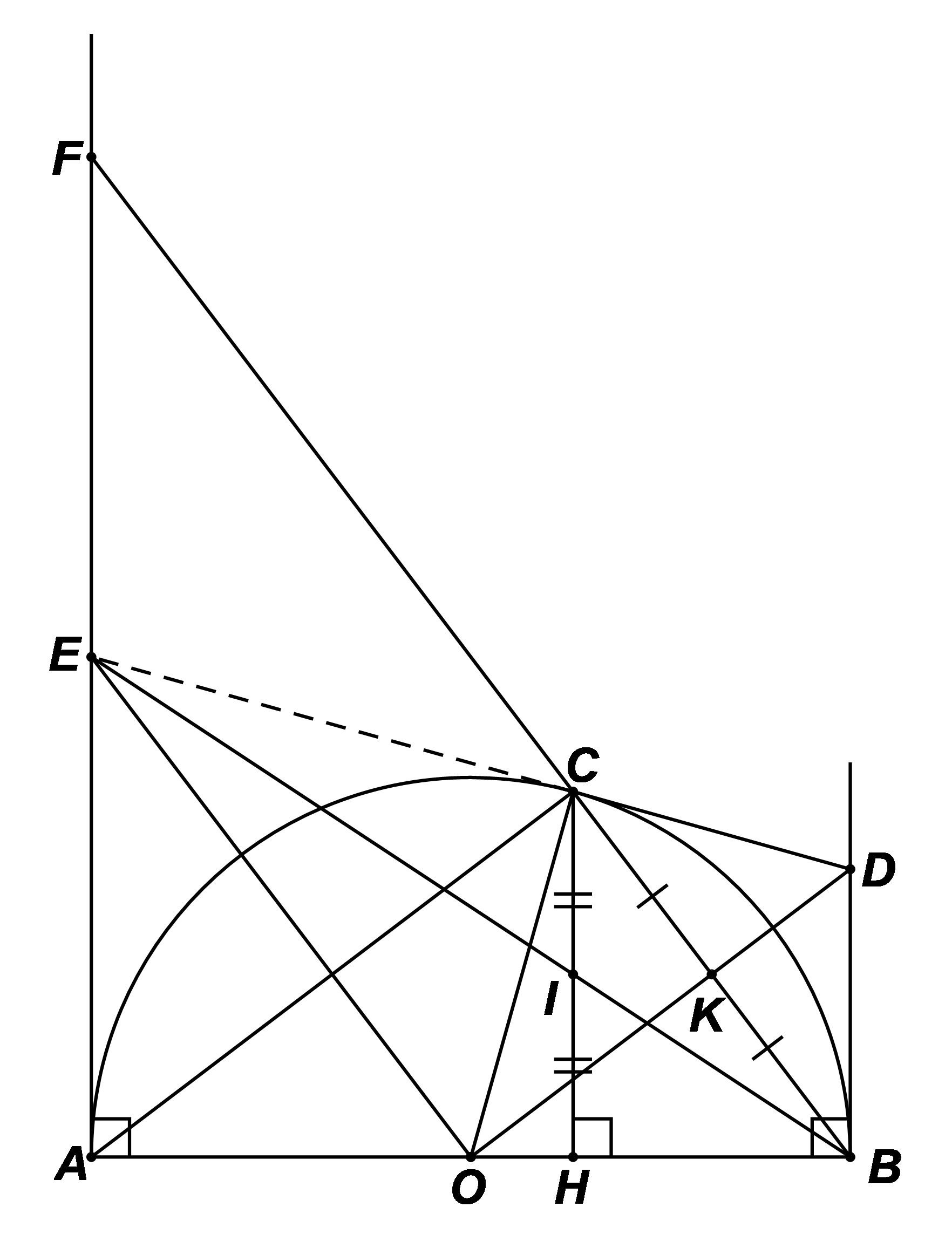Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Vòng đầu tiên của cuộc thi “Ai là Trạng Quỳnh” gồm bộ \(20\) câu hỏi, mỗi câu trả lời đúng được cộng \(8\) điểm, mỗi câu trả lời sai bị trừ \(4\) điểm. Mỗi thí sinh bắt đầu với \(10\) điểm và cần đạt ít nhất \(90\) điểm để vào vòng tiếp theo. Gọi \(x\) là số câu mà thí sinh cần trả lời đúng trong vòng đầu tiên \(\left( {x \in {\mathbb{N}^ * }} \right)\).
a) Số câu hỏi thí sinh trả lời sai trong vòng đầu tiên là \(20 - x\) câu.
b) Số điểm thí sinh có được khi xong vòng đầu tiên là \(10 + 8x + 4\left( {20 - x} \right)\) điểm.
c) Để qua vòng tiếp theo thì điểm của thí sinh phải thỏa mãn \(10 + 8x + 4\left( {20 - x} \right) > 90\).
d) Để qua vòng tiếp theo, mỗi thí sinh cần trả lời đúng ít nhất 14 câu.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Vòng đầu tiên của cuộc thi “Ai là Trạng Quỳnh” gồm bộ \(20\) câu hỏi, mỗi câu trả lời đúng được cộng \(8\) điểm, mỗi câu trả lời sai bị trừ \(4\) điểm. Mỗi thí sinh bắt đầu với \(10\) điểm và cần đạt ít nhất \(90\) điểm để vào vòng tiếp theo. Gọi \(x\) là số câu mà thí sinh cần trả lời đúng trong vòng đầu tiên \(\left( {x \in {\mathbb{N}^ * }} \right)\).
a) Số câu hỏi thí sinh trả lời sai trong vòng đầu tiên là \(20 - x\) câu.
b) Số điểm thí sinh có được khi xong vòng đầu tiên là \(10 + 8x + 4\left( {20 - x} \right)\) điểm.
c) Để qua vòng tiếp theo thì điểm của thí sinh phải thỏa mãn \(10 + 8x + 4\left( {20 - x} \right) > 90\).
d) Để qua vòng tiếp theo, mỗi thí sinh cần trả lời đúng ít nhất 14 câu.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: a) Đúng. b) Sai. c) Sai. d) Đúng.
• Gọi \(x\) là số câu mà thí sinh cần trả lời đúng trong vòng đầu tiên \(\left( {x \in {\mathbb{N}^ * }} \right)\).
Lúc này, số câu hỏi thí sinh trả lời sai trong vòng đầu tiên là: \(20 - x\) (câu).
Do đó, ý a) là đúng.
• Số điểm thí sinh nhận được khi trả lời đúng \(x\) câu hỏi là: \(8x\) (điểm).
Số điểm thí sinh bị trừ khi trả lời sai \(\left( {20 - x} \right)\) câu hỏi là: \(3\left( {20 - x} \right)\) (điểm).
Số điểm thí sinh có được khi thi xong vòng đầu tiên là: \(10 + 8x - 4\left( {20 - x} \right)\) (điểm).
Do đó, ý b) là sai.
• Theo bài, thí sinh cần đạt ít nhất \(90\) điểm để vào vòng tiếp theo nên ta có bất phương trình mô tả tình huống bài toán là: \(10 + 8x - 4\left( {20 - x} \right) \ge 90\).
Do đó, ý c) là sai.
• Giải bất phương trình:
\(10 + 8x - 4\left( {20 - x} \right) \ge 90\)
\(10 + 8x - 80 + 4x \ge 90\)
\(12x - 70 \ge 90\)
\(12x \ge 160\)
\(x \ge \frac{{160}}{{12}}\)
\(x \ge 13,33333.....\)
Do \(x \in {\mathbb{N}^ * }\) và cần tìm giá trị \(x\) nhỏ nhất nên \(x = 14.\)
Vậy để qua vòng tiếp theo, mỗi thí sinh cần trả lời đúng ít nhất là \(14\) câu.
Do đó, ý d) là đúng.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
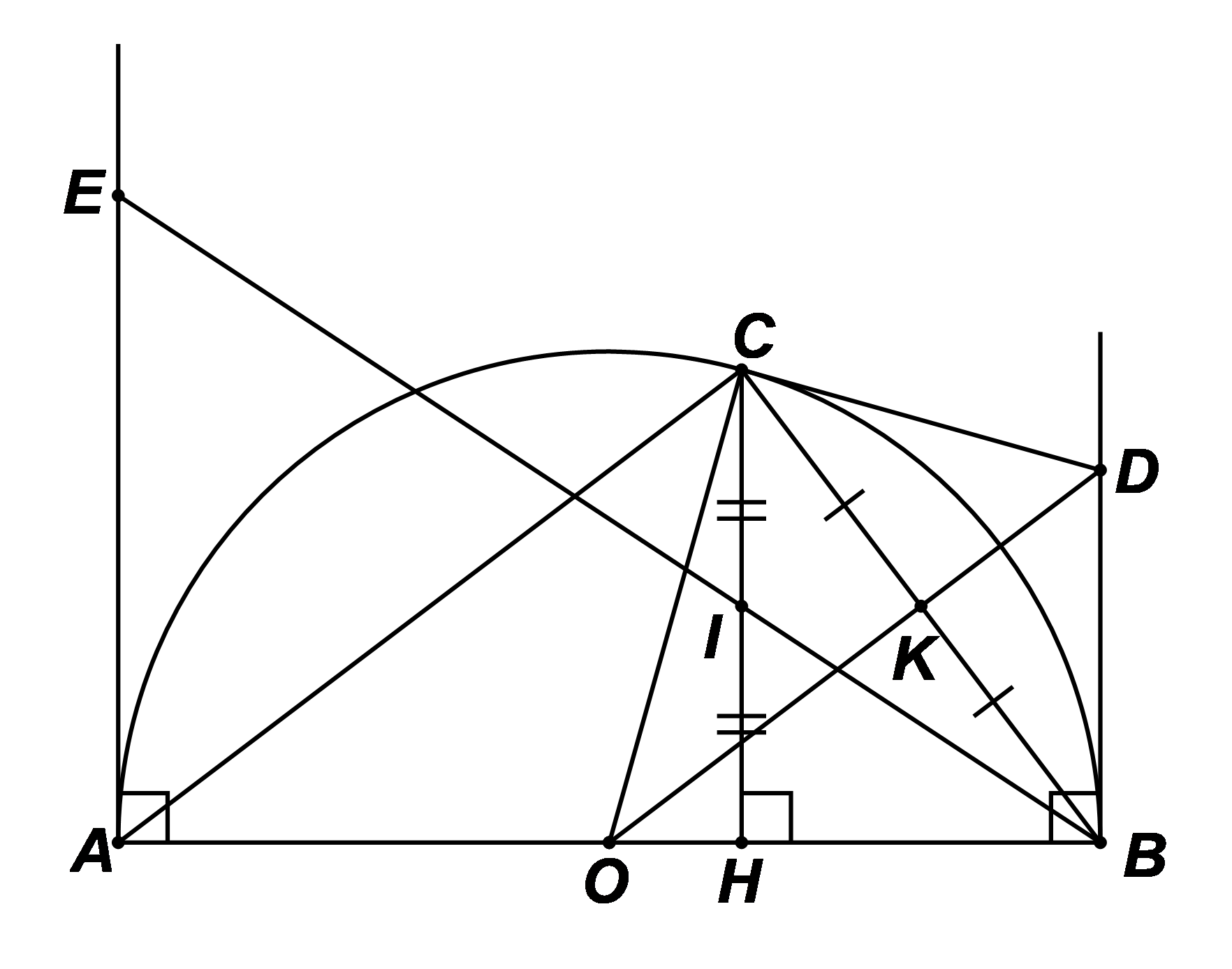
a) Xét \[\Delta OBC\] cân tại \[O\] (do \[OC = OB = R\]) nên đường trung tuyến \[OK\] cũng là đường cao của \[\Delta OBC.\] Suy ra \[OK \bot BC\] hay \[OD \bot BC\].
Xét nửa đường tròn \(\left( O \right)\) đường kính \(AB,\) có \[\widehat {ACB}\] là góc nội tiếp chắn nửa đường tròn nên \[\widehat {ACB} = 90^\circ .\]
Vậy \[\Delta ABC\] vuông tại \[C\].
b) Xét \[\Delta OBC\] cân tại \[O\] (do \[OC = OB = R\]) nên đường trung tuyến \[OK\] cũng là đường phân giác của \[\Delta OBC.\] Do đó \(\widehat {BOD} = \widehat {COD}.\)
Xét \[\Delta CDO\] và \[\Delta BDO\] có:
\[OD\] là cạnh chung; \(\widehat {BOD} = \widehat {COD}\); \[OB = OC\]
Do đó \[\Delta CDO = \Delta BDO\] (c.g.c).
Suy ra \[\widehat {DCO} = \widehat {DBO} = 90^\circ \] (hai góc tương ứng).
Như vậy, \[OC \bot DC\] tại \[C\] thuộc \(\left( O \right)\) hay \[DC\] là tiếp tuyến của đường tròn \[\left( O \right)\].
|
c) Gọi \[F\] là giao điểm của \[BC,\,\,AE.\] Ta có: \[IC \bot AB\] và \[AF \bot AB\], suy ra \[IC\,{\rm{//}}\,AF\] hay \[IC\,{\rm{//}}\,EF\]. Xét \[\Delta BEF\], có: \[\frac{{IC}}{{EF}} = \frac{{IB}}{{EB}}\] (Hệ quả định lí Thalès) (1) Xét \[\Delta BAE\], có: \[\frac{{IH}}{{AE}} = \frac{{IB}}{{EB}}\] (Hệ quả định lí Thalès) (2) Từ (1) và (2) suy ra \[\frac{{IC}}{{EF}} = \frac{{IH}}{{EA}}\], mà \[IC = IH\] (do \(I\) là trung điểm của \(CH)\) nên \[EF = EA\] hay \[E\] là trung điểm của \[AF.\] Ta có \[\widehat {FCA} = 90^\circ \] (cùng bù với \[\widehat {ACB} = 90^\circ \]) nên \[\Delta FCA\] vuông tại \[C\].
Xét \(\Delta ACF\) vuông tại \(C,\) có \(CE\) là đường trung tuyến ứng với cạnh huyền \(AF\) nên \[CE = EA = EF = \frac{1}{2}AF.\] Xét \[\Delta CEO\] và \[\Delta AEO\], có: \[CE = AE\], \[OC = OA\] và \[OE\] là cạnh chung Do đó \[\Delta CEO = \Delta AEO\] (c.c.c) Suy ra \[\widehat {ECO} = \widehat {EAO} = 90^\circ \] (hai góc tương ứng). Ta có: \[\widehat {ECO} + \widehat {OCD} = 90^\circ + 90^\circ = 180^\circ \] hay \[\widehat {ECD} = 180^\circ \]. Vậy ba điểm \[E,C,D\] thẳng hàng. |
|
Câu 2
A. \(x \ne 0;\,\,x \ne 1.\)
B. \(x \ne 0;\,\,x \ne - 1.\)
C. \(x \ne 3;\,\,x \ne 2.\)
D. \(x \ne 0.\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Điều kiện xác định của phương trình \(\frac{{x + 3}}{{x + 1}} + \frac{{x - 2}}{x} = 2\) là \(x + 1 \ne 0\) và \(x \ne 0\) hay \(x \ne - 1;\,\,x \ne 0.\)
Câu 3
A. \(\left\{ \begin{array}{l}3x - y = 5\\x + 2y = - 1\end{array} \right..\)
B. \(\left\{ \begin{array}{l} - 3y = 6\\3x + 5y = 15\end{array} \right..\)
C. \(\left\{ \begin{array}{l}{x^2} - 4{y^2} = 0\\2x + 5y = 7\end{array} \right..\)
D. \(\left\{ \begin{array}{l}2x - 3y = - 3\\2x + 5y = 7\end{array} \right..\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \({\left( { - \sqrt 5 } \right)^2}.\)
B. \(\sqrt {{5^2}} .\)
C. \(\sqrt {{{\left( { - 5} \right)}^2}} .\)
D. \( - {\left( {\sqrt 5 } \right)^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 1.
B. 2.
C. 3.
D. 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo