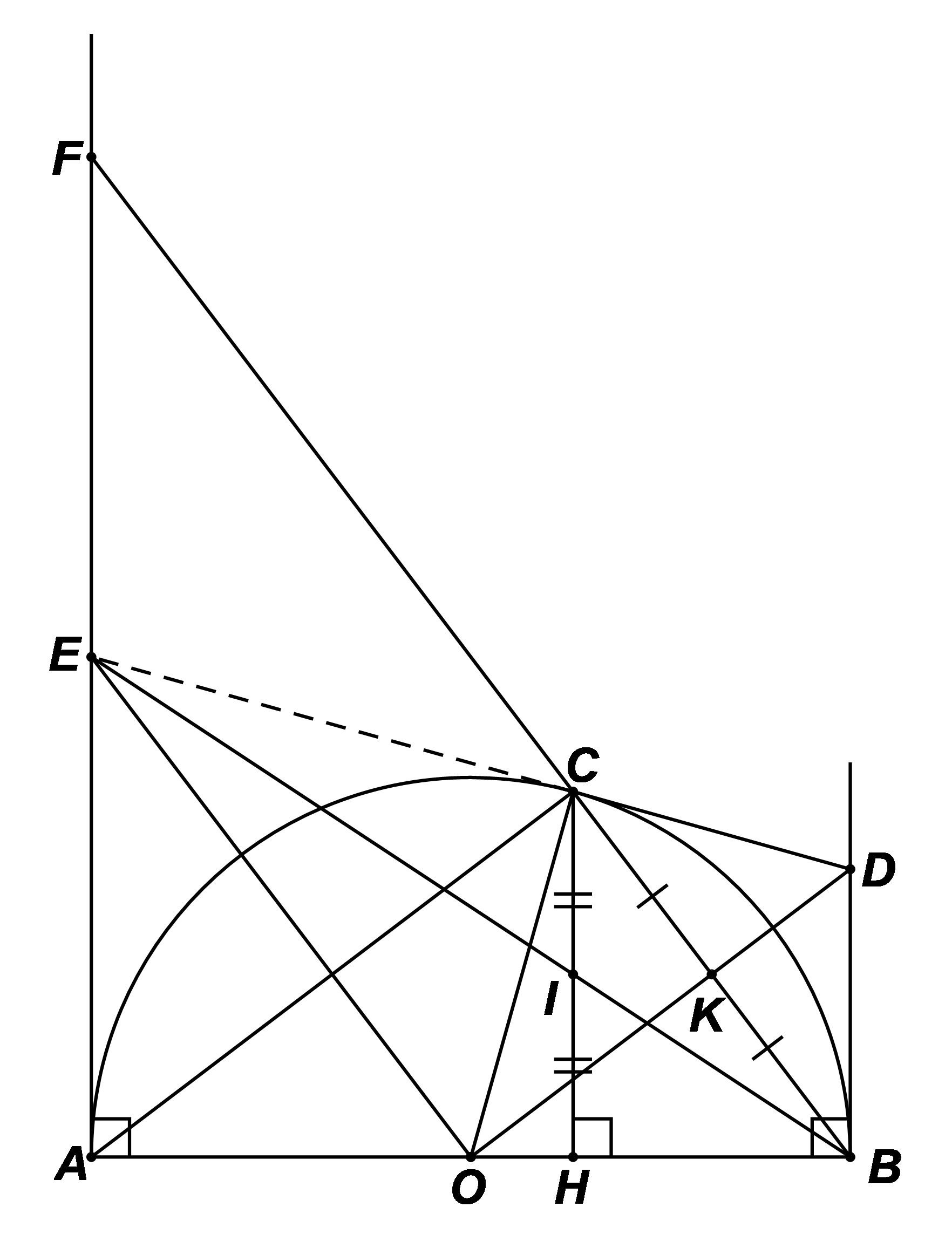Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Có bao nhiêu giá trị của \(x\) thỏa mãn phương trình: \(\frac{1}{{x - 2}} + 3 = \frac{{3 - x}}{{x - 2}}\)?
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Có bao nhiêu giá trị của \(x\) thỏa mãn phương trình: \(\frac{1}{{x - 2}} + 3 = \frac{{3 - x}}{{x - 2}}\)?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: 0
Điều kiện xác định: \(x \ne 2.\)
Ta có: \(\frac{1}{{x - 2}} + 3 = \frac{{3 - x}}{{x - 2}}\)
\(\frac{1}{{x - 2}} + \frac{{3\left( {x - 2} \right)}}{{x - 2}} = \frac{{3 - x}}{{x - 2}}\)
\(\frac{{1 + 3\left( {x - 2} \right)}}{{x - 2}} = \frac{{3 - x}}{{x - 2}}\)
\(1 + 3\left( {x - 2} \right) = 3 - x\)
\(1 + 3x - 6 = 3 - x\)
\(3x - 5 = 3 - x\)
\(4x = 8\)
\(x = 2.\)
Mà điều kiện xác định \(x \ne 2\) nên phương trình không có giá trị thỏa mãn.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
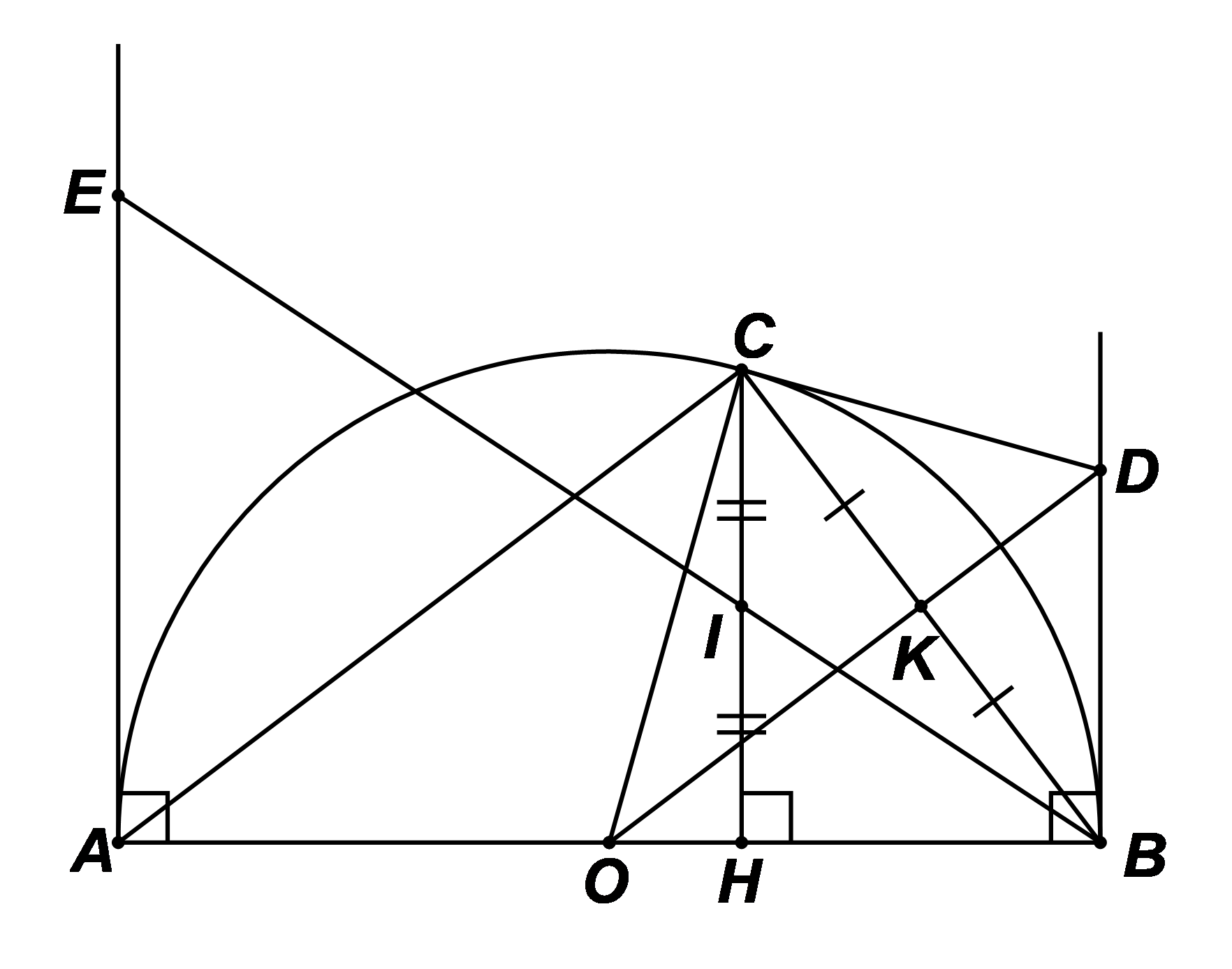
a) Xét \[\Delta OBC\] cân tại \[O\] (do \[OC = OB = R\]) nên đường trung tuyến \[OK\] cũng là đường cao của \[\Delta OBC.\] Suy ra \[OK \bot BC\] hay \[OD \bot BC\].
Xét nửa đường tròn \(\left( O \right)\) đường kính \(AB,\) có \[\widehat {ACB}\] là góc nội tiếp chắn nửa đường tròn nên \[\widehat {ACB} = 90^\circ .\]
Vậy \[\Delta ABC\] vuông tại \[C\].
b) Xét \[\Delta OBC\] cân tại \[O\] (do \[OC = OB = R\]) nên đường trung tuyến \[OK\] cũng là đường phân giác của \[\Delta OBC.\] Do đó \(\widehat {BOD} = \widehat {COD}.\)
Xét \[\Delta CDO\] và \[\Delta BDO\] có:
\[OD\] là cạnh chung; \(\widehat {BOD} = \widehat {COD}\); \[OB = OC\]
Do đó \[\Delta CDO = \Delta BDO\] (c.g.c).
Suy ra \[\widehat {DCO} = \widehat {DBO} = 90^\circ \] (hai góc tương ứng).
Như vậy, \[OC \bot DC\] tại \[C\] thuộc \(\left( O \right)\) hay \[DC\] là tiếp tuyến của đường tròn \[\left( O \right)\].
|
c) Gọi \[F\] là giao điểm của \[BC,\,\,AE.\] Ta có: \[IC \bot AB\] và \[AF \bot AB\], suy ra \[IC\,{\rm{//}}\,AF\] hay \[IC\,{\rm{//}}\,EF\]. Xét \[\Delta BEF\], có: \[\frac{{IC}}{{EF}} = \frac{{IB}}{{EB}}\] (Hệ quả định lí Thalès) (1) Xét \[\Delta BAE\], có: \[\frac{{IH}}{{AE}} = \frac{{IB}}{{EB}}\] (Hệ quả định lí Thalès) (2) Từ (1) và (2) suy ra \[\frac{{IC}}{{EF}} = \frac{{IH}}{{EA}}\], mà \[IC = IH\] (do \(I\) là trung điểm của \(CH)\) nên \[EF = EA\] hay \[E\] là trung điểm của \[AF.\] Ta có \[\widehat {FCA} = 90^\circ \] (cùng bù với \[\widehat {ACB} = 90^\circ \]) nên \[\Delta FCA\] vuông tại \[C\].
Xét \(\Delta ACF\) vuông tại \(C,\) có \(CE\) là đường trung tuyến ứng với cạnh huyền \(AF\) nên \[CE = EA = EF = \frac{1}{2}AF.\] Xét \[\Delta CEO\] và \[\Delta AEO\], có: \[CE = AE\], \[OC = OA\] và \[OE\] là cạnh chung Do đó \[\Delta CEO = \Delta AEO\] (c.c.c) Suy ra \[\widehat {ECO} = \widehat {EAO} = 90^\circ \] (hai góc tương ứng). Ta có: \[\widehat {ECO} + \widehat {OCD} = 90^\circ + 90^\circ = 180^\circ \] hay \[\widehat {ECD} = 180^\circ \]. Vậy ba điểm \[E,C,D\] thẳng hàng. |
|
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đúng. b) Sai. c) Sai. d) Đúng.
• Gọi \(x\) là số câu mà thí sinh cần trả lời đúng trong vòng đầu tiên \(\left( {x \in {\mathbb{N}^ * }} \right)\).
Lúc này, số câu hỏi thí sinh trả lời sai trong vòng đầu tiên là: \(20 - x\) (câu).
Do đó, ý a) là đúng.
• Số điểm thí sinh nhận được khi trả lời đúng \(x\) câu hỏi là: \(8x\) (điểm).
Số điểm thí sinh bị trừ khi trả lời sai \(\left( {20 - x} \right)\) câu hỏi là: \(3\left( {20 - x} \right)\) (điểm).
Số điểm thí sinh có được khi thi xong vòng đầu tiên là: \(10 + 8x - 4\left( {20 - x} \right)\) (điểm).
Do đó, ý b) là sai.
• Theo bài, thí sinh cần đạt ít nhất \(90\) điểm để vào vòng tiếp theo nên ta có bất phương trình mô tả tình huống bài toán là: \(10 + 8x - 4\left( {20 - x} \right) \ge 90\).
Do đó, ý c) là sai.
• Giải bất phương trình:
\(10 + 8x - 4\left( {20 - x} \right) \ge 90\)
\(10 + 8x - 80 + 4x \ge 90\)
\(12x - 70 \ge 90\)
\(12x \ge 160\)
\(x \ge \frac{{160}}{{12}}\)
\(x \ge 13,33333.....\)
Do \(x \in {\mathbb{N}^ * }\) và cần tìm giá trị \(x\) nhỏ nhất nên \(x = 14.\)
Vậy để qua vòng tiếp theo, mỗi thí sinh cần trả lời đúng ít nhất là \(14\) câu.
Do đó, ý d) là đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 1.
B. 2.
C. 3.
D. 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập