Ném còn là một trò chơi dân gian Việt Nam phổ biến trong các dịp lễ hội đầu năm của các dân tộc Tày, Thái, Mường, chủ yếu ở vùng Tây Bắc. Ý nghĩa của trò chơi là cầu mong mùa màng tươi tốt, vạn vật sinh sôi nảy nở và cầu mong giao hoà âm dương, đất trời.

Trò chơi gồm một cây cọc thẳng lớn, thường làm bằng thân tre khá cao và có gắn một vòng tròn lớn trên ngọn. Cọc được đặt ở một sân bãi rộng rãi. Quả còn (trái còn) làm bằng vải nhiều màu chứa hạt bông, thóc hoặc cát, dây lược gắn với quả còn dài \(50 - 60\;{\rm{cm}}\). Người chơi đứng cách cây cọc một khoảng cách tương đối, sau đó cầm dây lược ném quả còn làm sao cho quả bay qua vòng tròn trên cây cọc là chiến thắng.

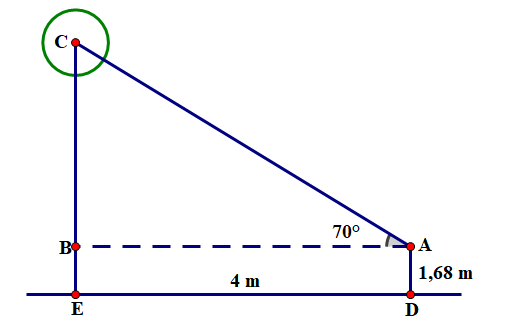
Tại lễ hội năm nay, một người chơi ném còn đứng cách chân cọc một khoảng \[4{\rm{ m}}\] và góc nâng từ tầm mắt đến đỉnh ngọn cọc là \(70^\circ .\) Biết rằng chiều cao từ mặt đất đến mắt người này là \[1,68{\rm{ m}}.\] Tính chiều cao của cọc (kết quả làm tròn đến hàng phần mười) (đơn vị: mét).

                                     

 

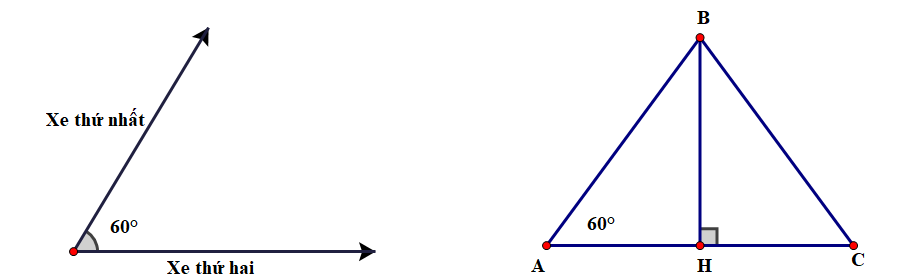
Do mặt đất là phương ngang nên \[\widehat {BCA} = 30^\circ \] và \[\widehat {BDA} = 60^\circ \].

Gọi \[x\] (m/phút) là vận tốc xe máy, điều kiện \[x > 0\].

Vì xe máy đi từ \[C\] đến \[D\] trong \[6\] phút nên \[CD = 6x\,\,\left( {\rm{m}} \right)\]

• Xét \[\Delta ABC\] vuông tại \[A\], ta có:

\[AC = AB \cdot \cot \widehat {BCA} = AB \cdot \cot 30^\circ  = AB \cdot \tan 60^\circ  = \sqrt 3 AB\] (do \[\cot 30^\circ  = \tan 60^\circ \]) \[\left( 1 \right)\]

• Xét \[\Delta ABD\] vuông tại \[A\], ta có:

\[AD = AB \cdot \,\cot \widehat {BDA} = AB \cdot \,\cot 60^\circ  = AB \cdot \tan 30^\circ  = \frac{{\sqrt 3 AB}}{3}\] (do \[\cot 60^\circ  = \tan 30^\circ \]) \[\left( 2 \right)\]

Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[AC - AD = AB\left( {\sqrt 3  - \frac{{\sqrt 3 }}{3}} \right)\] nên \[CD = \frac{{2\sqrt 3 }}{3}AB\].

Ta có \[\frac{{AD}}{{CD}} = \frac{{\sqrt 3 AB}}{3}:\frac{{2\sqrt 3 }}{3}AB = \frac{1}{2}\].

Suy ra \[AD = \frac{1}{2}CD = \frac{1}{2} \cdot 6x = 3x\,\,({\rm{m}}).\]

Vậy thời gian để xe máy chạy từ \[D\] đến tòa nhà là \[\frac{{3x}}{x} = 3\] (phút).

Đáp án: 3.

Chọn C

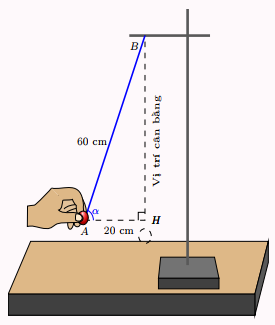
Gắn dữ kiện của bài toán vào mô hình Toán học như trên hình vẽ.

Gọi \[N\] là hình chiếu của \[M\] lên đoạn \[AH\].

Vì \[MN\] và \[BH\] là các đoạn thẳng nằm trên phương ngang; \[MB\] và \[NH\] nằm trên phương thẳng đứng nên tứ giác \[MBHN\] là hình chữ nhật.

Suy ra \[NH = MB = 1,55\,\,{\rm{m}}\]; \[MN = BH = 13,65\,\,{\rm{m}}\].

Tam giác \[ANM\] vuông tại \[N\] nên \[AN = MN \cdot \tan M.\]

Ta có:\[AH = AN + NH\]suy ra \[AH = MN \cdot \tan M + NH\].

Do đó \[AH = 13,65 \cdot \tan 58^\circ  + 1,55 \approx 23,39\,\,({\rm{m}}).\]

Vậy chiều cao của tháp khoảng \[23,39\,\,{\rm{m}}\].