Phần I. Trắc nghiệm nhiều phương án lựa chọn
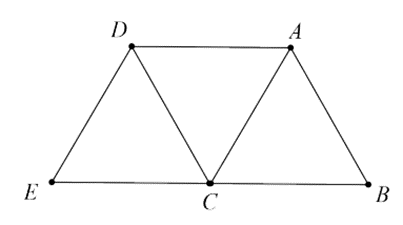
Khẳng định nào dưới đây là sai khi nói về tam giác đều?
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Khẳng định nào dưới đây là sai khi nói về tam giác đều?
Quảng cáo
Trả lời:
Đáp án đúng là: B
Tam giác đều không có tâm đối xứng do đó đáp án B là sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 18
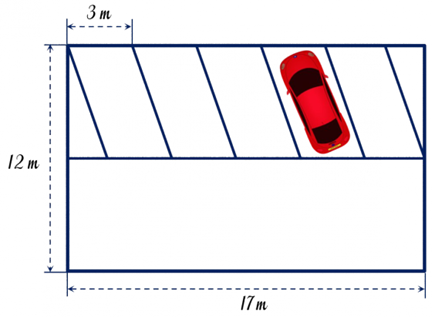
Chiều cao của chỗ đậu xe cho một ô tô là \(12:2 = 6{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\)
Diện tích ô dành cho một xe đậu là: \(3 \cdot 6 = 18{\rm{ }}\left( {{{\rm{m}}^2}} \right){\rm{.}}\)
Lời giải
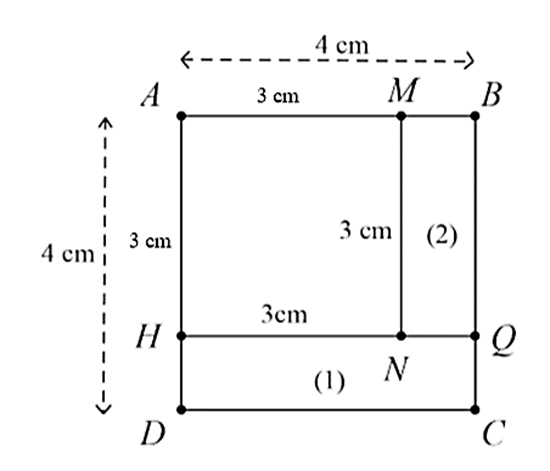
a) Sai
Chu vi một cánh hoa là: \(4 \cdot 4 = 16{\rm{ }}\left( {{\rm{cm}}} \right)\).
b) Sai.
Chu vi một chiếc lá là: \(4 \cdot 3 = 12{\rm{ }}\left( {{\rm{cm}}} \right)\).
Do đó, chu vi một cánh hoa lớn hơn chu vi một chiếc lá.
c) Đúng.
Có tất cả 6 cánh hoa.
Do đó, tổng chu vi giấy màu để làm tất cả cánh hoa cho bông hoa đó là: \(16 \cdot 4 = 64{\rm{ }}\left( {{\rm{cm}}} \right)\).
d) Đúng.
Có hai chiếc lá.
Do đó, tổng chu vi giấy màu để làm lá cho bông hoa đó là: \(12 \cdot 2 = 24{\rm{ }}\left( {{\rm{cm}}} \right)\).
Vậy tổng chu vi giấy màu để làm cánh hoa và lá của bông hoa đó là: \(24 + 64 = 88{\rm{ }}\left( {{\rm{cm}}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.