Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông, \(SA\)vuông góc với mặt phẳng \((ABCD)\). Gọi \[I,J\] lần lượt là trung điểm của \[SA,SC\]. \[G\]là trọng tâm tam giác \[SBD\].
![Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là h (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/15-1761392134.png)
a) \(\overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {AD} \).
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \).
c) \[\overrightarrow {{\rm{IJ}}} .\overrightarrow {BD} = \overrightarrow 0 \].
d) \({\overrightarrow {AG} ^2} = {\overrightarrow {AS} ^2} + {\overrightarrow {AB} ^2} + {\overrightarrow {AD} ^2}\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông, \(SA\)vuông góc với mặt phẳng \((ABCD)\). Gọi \[I,J\] lần lượt là trung điểm của \[SA,SC\]. \[G\]là trọng tâm tam giác \[SBD\].
![Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là h (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/15-1761392134.png)
a) \(\overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {AD} \).
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \).
c) \[\overrightarrow {{\rm{IJ}}} .\overrightarrow {BD} = \overrightarrow 0 \].
d) \({\overrightarrow {AG} ^2} = {\overrightarrow {AS} ^2} + {\overrightarrow {AB} ^2} + {\overrightarrow {AD} ^2}\).
Quảng cáo
Trả lời:
a) Ta có \[ABCD\] là hình vuông nên \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \) ( qui tắc hình bình hành)
suy ra\(\overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {AD} \).
b) Do \[G\]là trọng tâm tam giác \[SBD\] nên
\(\overrightarrow {GS} + \overrightarrow {GB} + \overrightarrow {GD} = \overrightarrow 0 \Rightarrow \left( {\overrightarrow {GA} + \overrightarrow {AS} } \right) + \left( {\overrightarrow {GA} + \overrightarrow {AB} } \right) + \left( {\overrightarrow {GA} + \overrightarrow {AD} } \right) = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = 3\overrightarrow {AG} .\)
c) Ta có \[ABCD\] là hình vuông nên \(AC \bot BD \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = 0 \Rightarrow 2\overrightarrow {{\rm{IJ}}} .\overrightarrow {BD} = 0 \Rightarrow \overrightarrow {{\rm{IJ}}} .\overrightarrow {BD} = 0\) .
Mà \[\overrightarrow 0 \ne 0\] nên mệnh đề sai.
d) Do \[G\]là trọng tâm tam giác \[SBD\] nên \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = 3\overrightarrow {AG} \)
\({\left( {3\overrightarrow {AG} } \right)^2} = {\left( {\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} } \right)^2} \Rightarrow 9A{G^2} = A{S^2} + A{B^2} + A{D^2} + 2\overrightarrow {AS} \overrightarrow {AB} + 2\overrightarrow {AS} \overrightarrow {AD} + 2\overrightarrow {AD} \overrightarrow {AB} \;\left( 1 \right)\)
Vì \(SA\)vuông góc với mặt phẳng \((ABCD)\) nên\(\left\{ \begin{array}{l}SA \bot AB\\SA \bot AD\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {SA} .\overrightarrow {AD} = 0\\\overrightarrow {SA} .\overrightarrow {AB} = 0\end{array} \right.\;\left( 2 \right)\)
\[ABCD\] là hình vuông nên \(\overrightarrow {AB} .\overrightarrow {AD} = 0\left( 3 \right)\) .
Từ \[\left( 1 \right);\left( 2 \right);\left( 3 \right)\] ta được \(9A{G^2} = A{S^2} + A{B^2} + A{D^2}.\)
Đáp án: a) Đúng; b) Sai; c) Sai; d) Sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
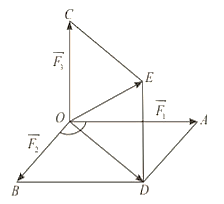
a) Có \(OADB\) là hình bình hành nên \(\overrightarrow {BO} + \overrightarrow {BD} = \overrightarrow {BA} \) (quy tắc hình bình hành).
b) Có \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OD} ;\overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {OE} \).
Do đó \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OE} \).
c) Vì \(OADB\) là hình bình hành và \(\widehat {BOA} = 120^\circ \Rightarrow \widehat {OBD} = 60^\circ \).
Xét \(\Delta OBD\) có \(OD = \sqrt {O{B^2} + B{D^2} - 2.OB.BD.\cos 60^\circ } = \sqrt {{{24}^2} + {{12}^2} - 2.24.12.\cos 60^\circ } = 12\sqrt 3 \) N.
d) Ta có \(\Delta OCE\) vuông tại \(C\), ta có \(OE = \sqrt {O{C^2} + C{E^2}} = \sqrt {{6^2} + {{\left( {12\sqrt 3 } \right)}^2}} = 6\sqrt {13} \) N.
Đáp án: a) Sai; b) Đúng; c) Sai; d) Đúng.
Câu 2
Lời giải
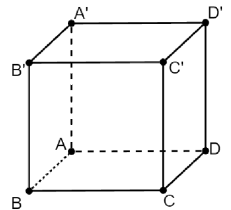
Ta có: \(\overrightarrow {BD} \, = \,\,\overrightarrow {B'D'} \).
Do đó,\(\left( {\overrightarrow {BD} \,,\,\overrightarrow {B'C} } \right)\, = \,\left( {\overrightarrow {B'D'} \,,\,\overrightarrow {B'C} } \right)\, = \widehat {\,D'B'C}\)
Vì \(B'C = \,CD'\, = \,D'B'\)nên tam giác \(B'CD'\)là tam giác đều.
Suy ra \(\widehat {\,D'B'C}\, = \,60^\circ \).
Vậy \(\left( {\overrightarrow {BD} \,,\,\overrightarrow {B'C} } \right)\, = \,60^\circ \). Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.