Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất 8000 quả bóng tennis. Biết công ty này có 38 máy và mỗi máy có thể sản xuất 30 quả bóng trong một giờ. Chi phí thiết lập các máy này là 200 nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giảm sát. Số tiền phải trả cho người giám sát là 192 nghìn đồng một giờ. Số máy công ty nên sử dụng để sản xuất đơn hàng trên là bao nhiêu để chi phí hoạt động là thấp nhất?
Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất 8000 quả bóng tennis. Biết công ty này có 38 máy và mỗi máy có thể sản xuất 30 quả bóng trong một giờ. Chi phí thiết lập các máy này là 200 nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giảm sát. Số tiền phải trả cho người giám sát là 192 nghìn đồng một giờ. Số máy công ty nên sử dụng để sản xuất đơn hàng trên là bao nhiêu để chi phí hoạt động là thấp nhất?
Quảng cáo
Trả lời:
Gọi \(x\) là số máy công ty sử dụng để sản xuất đơn hàng 8000 quả bóng tennis, \(x \in \left( {0;38} \right],x \in \mathbb{N}\).
Số bóng mỗi máy cần sản xuất: \(\frac{{8000}}{x}\).
Số giờ cần thiết để hoàn thành đơn hàng \(\frac{{8000}}{{30x}} = \frac{{800}}{{3x}}\).
Chi phí hoạt động: \(f\left( x \right) = 200x + 192.\frac{{800}}{{3x}} = 200x + \frac{{51200}}{x}\)(nghìn đồng).
Ta có \(f'\left( x \right) = 200 - \frac{{51200}}{{{x^2}}}\); \(f'\left( x \right) = 0 \Leftrightarrow 200 - \frac{{51200}}{{{x^2}}} = 0 \Leftrightarrow {x^2} = 256 \Leftrightarrow x = 16\) vì \(x \in \left( {0;38} \right],x \in \mathbb{N}\).
Bảng biến thiên:
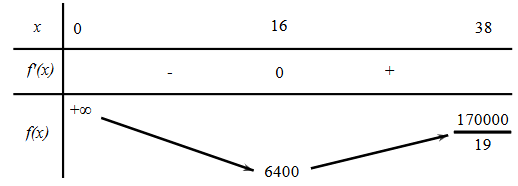
Suy ra \(\mathop {\min }\limits_{\left( {0;38} \right]} f\left( x \right) = 6400\) khi \(x = 16\).
Vậy công ty nên sử dụng 16 máy để sản xuất đơn hàng 8000 quả bóng tennis cho chi phí hoạt động là thấp nhất.
Trả lời: 16.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số tiền thu về khi bán \(x\) mét vải lụa là: \(220x\).
Lợi nhuận thu được khi bán \(x\) mét vải lụa là:
\(L\left( x \right) = 220x - \left( {{x^3} - 3{x^2} - 20x + 500} \right) = - {x^3} + 3{x^2} + 240x - 500\).
Xét hàm số \(L\left( x \right) = - {x^3} + 3{x^2} + 240x - 500\) với \(x \in \left[ {1;18} \right]\)
\(L'\left( x \right) = - 3{x^2} + 6x + 240 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 10 \in [1;18]\\x = - 8 \notin [1;18]\end{array} \right.\)\(\)
Bảng biến thiên:
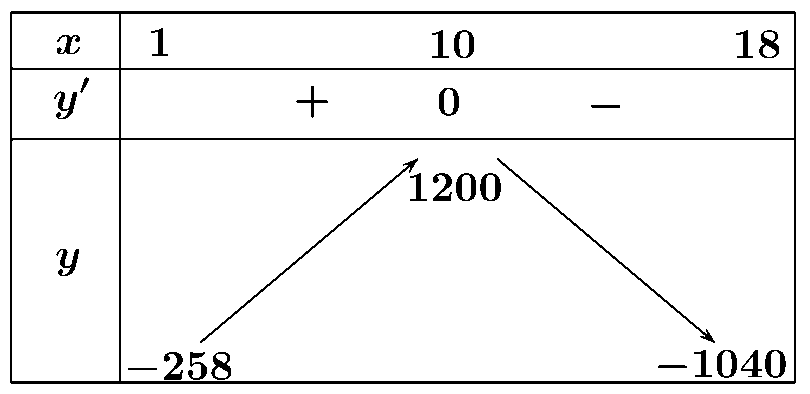
Vậy hộ làm nghề dệt này thu được lợi nhuận tối đa trong một ngày là \(1200\) nghìn đồng khi sản xuất \(10\) mét vải lụa trong một ngày.
Trả lời: 1200.
Lời giải
a) Chi phí mỗi ngày là tổng các chi phí nên \(C\left( x \right) = 0,0005{x^2} + 0,15x + 5\) (triệu đồng).
b) Khi \(x = 100\), ta có \(C\left( {100} \right) = 0,0005 \times {100^2} + 0,15 \times 100 + 5 = 25\).
c) Chi phí trung bình trên mỗi khối sản phẩm là:
\(\overline c \left( x \right) = \frac{{0,0005{x^2} + 0,15x + 5}}{x} = 0,0005x + 0,15 + \frac{5}{x}\).
d) Xét hàm số \(\overline c \left( x \right) = 0,0005x + 0,15 + \frac{5}{x}\), \(0 < x \le 200\).
Ta có \({\overline c ^{\,\prime }}\left( x \right) = \frac{5}{{{{10}^4}}} - \frac{5}{{{x^2}}}\), \({\overline c ^\prime }\left( x \right) = 0 \Leftrightarrow {x^2} = {10^4} \Rightarrow x = 100\) (do \(x \in \left( {0;200} \right]\))
Bảng biến thiên:
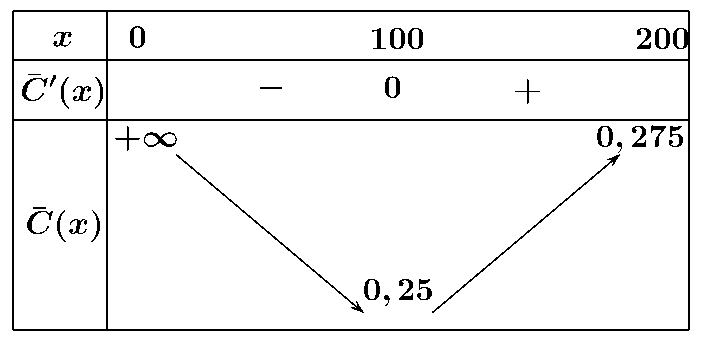
Vậy chi phí trung bình giảm khi hàm số \(\overline c \left( x \right)\)nghịch biến, tức là \(x \in \left( {0;100} \right)\).
Đáp án: a) Đúng; b) Sai; c) Đúng; d) Đúng.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.