Đề cương ôn tập cuối kì 1 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn
43 người thi tuần này 4.6 1.4 K lượt thi 12 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1
Lời giải
Ta có: \(S = {t^3} - 3{t^2} - 9t + 2\).
\( \Rightarrow \left\{ \begin{array}{l}v = S' = 3{t^2} - 6t - 9\\a = S'' = 6t - 6\end{array} \right.\)
Khi vận tốc bị triệt tiêu tức \(v = 0 \Leftrightarrow 3{t^2} - 6t - 9 = 0 \Leftrightarrow \left[ \begin{array}{l}t = - 1 < 0\\t = 3\left( {tm} \right)\end{array} \right.\).
Khi đó gia tốc tại thời điểm vận tốc bị triệt tiêu là \(a = 6.3 - 6 = 12\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\). Chọn D.
Câu 2
Lời giải
Vì \[s = \frac{1}{3}{t^3} - {t^2} + 9t \Rightarrow v = {t^2} - 2t + 9\].
Xét hàm \[f\left( t \right) = {t^2} - 2t + 9 \Rightarrow f'\left( t \right) = 2t - 2 = 0 \Rightarrow t = 1\].
Bảng biến thiên
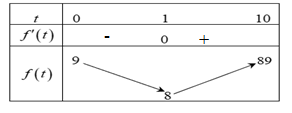
Dựa vào bảng biến thiên ta thấy: \[\mathop {\max }\limits_{\left[ {0;10} \right]} f\left( t \right) = f\left( {10} \right) = 89\].
Vậy vận tốc của vật đạt được lớn nhất bằng \[89\left( {{\rm{m/s}}} \right).\] Chọn A.
Câu 3
Lời giải
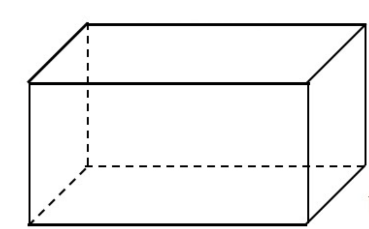
Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là \(x,\,2x,\,y\,\left( {x,\,y > 0} \right)\).
Diện tích phần lắp kính là
\(2x.x + 2xy + 2.2x.y = 2{x^2} + 6xy = 8\, \Leftrightarrow \,xy = \frac{{8 - 2{x^2}}}{6} > 0\) \( \Rightarrow \,x < \sqrt {\frac{8}{2}} = \sqrt 4 = 2\).
Thể tích bể cá là: \(V = 2x.x.y = 2x.\frac{{8 - 2{x^2}}}{6} = \frac{{ - 4{x^3} + 16x}}{6}\) với \(0 < x < 2\).
Ta có: \(V' = \frac{{ - 12{x^2} + 16}}{6},\,V' = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{2}{{\sqrt 3 }}\\x = - \frac{2}{{\sqrt 3 }}\,\,\left( L \right)\end{array} \right.\)
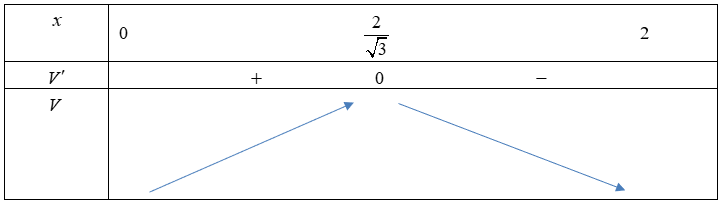
\( \Rightarrow \,{V_{\max }} = V\left( {\frac{2}{{\sqrt 3 }}} \right) \approx \,2,05\,{{\rm{m}}^{\rm{3}}}\). Chọn A.
Câu 4
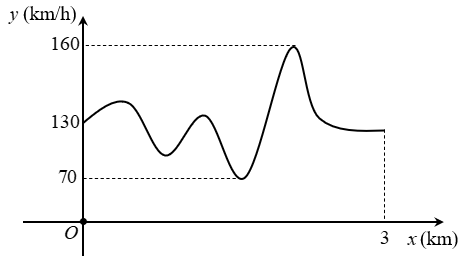
A. \(3\,\)(km/h).
Lời giải
Dựa vào đồ thị ta thấy tốc độ nhỏ nhất bằng \(70\)(km/h). Chọn D.
Câu 5
Lời giải
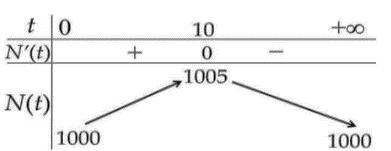
Tốc độ tăng trưởng của quần thể nấm \(X\) tại thời điểm \(t\) là: \[P'\left( t \right) = 120.0,15.{{\rm{e}}^{0,15t}} = 18{{\rm{e}}^{0,15t}}\].
Do đó, tốc độ tăng trưởng của quần thể nấm \(X\) tại thời điểm \(t = 0\) là \[P'\left( 0 \right) = 18\] tế bào/giờ. Chọn A.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.