Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức \(N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\) (con), trong đó \(t\) là thời gian tính bằng giây.
a) Đến giây thứ 10 thì số lượng vi khuẩn đạt nhiều nhất.
b) Thời gian tăng lên nhiều giờ thì số lượng vi khuẩn càng nhiều.
c) Sau khi cấy lại môi trường dinh dưỡng, số lượng vi khuẩn tăng thêm được 3 con so với lúc đầu tại hai thời điểm \({t_1}\) và \({t_2}\). Khi đó \({t_1}{t_2} = 100\).
d) Bảng biến thiên của hàm số \(N\left( t \right)\) như hình
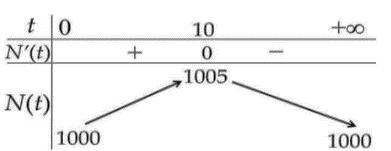
Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức \(N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\) (con), trong đó \(t\) là thời gian tính bằng giây.
a) Đến giây thứ 10 thì số lượng vi khuẩn đạt nhiều nhất.
b) Thời gian tăng lên nhiều giờ thì số lượng vi khuẩn càng nhiều.
c) Sau khi cấy lại môi trường dinh dưỡng, số lượng vi khuẩn tăng thêm được 3 con so với lúc đầu tại hai thời điểm \({t_1}\) và \({t_2}\). Khi đó \({t_1}{t_2} = 100\).
d) Bảng biến thiên của hàm số \(N\left( t \right)\) như hình

Quảng cáo
Trả lời:
Ta có \(N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\) nên \(N'\left( t \right) = \frac{{ - 100{t^2} + 10000}}{{{{\left( {{t^2} + 100} \right)}^2}}}\).
Do đó \(N'\left( t \right) = 0 \Leftrightarrow t = 10\).
a) Ta có \(N\left( 0 \right) = 1000;N\left( {10} \right) = 1005\) và \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right) = 1000\) nên \(\mathop {\max }\limits_{\left[ {0; + \infty } \right)} N\left( t \right) = N\left( {10} \right) = 1005\).
b) Có \(N'\left( t \right) < 0 \Leftrightarrow t > 10\).
c) Có \(N\left( t \right) = 1003 \Leftrightarrow \frac{{100t}}{{{t^2} + 100}} = 3\) \( \Leftrightarrow 3{t^2} - 100t + 300 = 0\).
Phương trình trên có hai nghiệm phân biệt \({t_1};{t_2}\) và \({t_1}{t_2} = 100\).
d) Bảng biến thiên

Đáp án: a) Đúng; b) Sai; c) Đúng; d) Đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số tiền thu về khi bán \(x\) mét vải lụa là: \(220x\).
Lợi nhuận thu được khi bán \(x\) mét vải lụa là:
\(L\left( x \right) = 220x - \left( {{x^3} - 3{x^2} - 20x + 500} \right) = - {x^3} + 3{x^2} + 240x - 500\).
Xét hàm số \(L\left( x \right) = - {x^3} + 3{x^2} + 240x - 500\) với \(x \in \left[ {1;18} \right]\)
\(L'\left( x \right) = - 3{x^2} + 6x + 240 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 10 \in [1;18]\\x = - 8 \notin [1;18]\end{array} \right.\)\(\)
Bảng biến thiên:
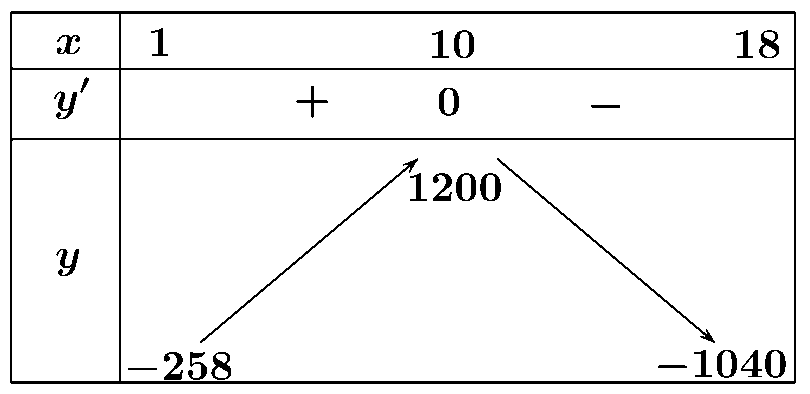
Vậy hộ làm nghề dệt này thu được lợi nhuận tối đa trong một ngày là \(1200\) nghìn đồng khi sản xuất \(10\) mét vải lụa trong một ngày.
Trả lời: 1200.
Lời giải
a) Chi phí mỗi ngày là tổng các chi phí nên \(C\left( x \right) = 0,0005{x^2} + 0,15x + 5\) (triệu đồng).
b) Khi \(x = 100\), ta có \(C\left( {100} \right) = 0,0005 \times {100^2} + 0,15 \times 100 + 5 = 25\).
c) Chi phí trung bình trên mỗi khối sản phẩm là:
\(\overline c \left( x \right) = \frac{{0,0005{x^2} + 0,15x + 5}}{x} = 0,0005x + 0,15 + \frac{5}{x}\).
d) Xét hàm số \(\overline c \left( x \right) = 0,0005x + 0,15 + \frac{5}{x}\), \(0 < x \le 200\).
Ta có \({\overline c ^{\,\prime }}\left( x \right) = \frac{5}{{{{10}^4}}} - \frac{5}{{{x^2}}}\), \({\overline c ^\prime }\left( x \right) = 0 \Leftrightarrow {x^2} = {10^4} \Rightarrow x = 100\) (do \(x \in \left( {0;200} \right]\))
Bảng biến thiên:
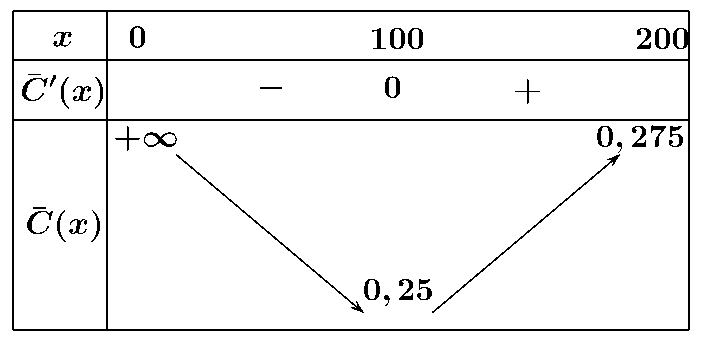
Vậy chi phí trung bình giảm khi hàm số \(\overline c \left( x \right)\)nghịch biến, tức là \(x \in \left( {0;100} \right)\).
Đáp án: a) Đúng; b) Sai; c) Đúng; d) Đúng.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.