Đề cương ôn tập cuối kì 1 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Tự luận

Ta có: \(f'(x) = 3{x^2} - 12x + 9\);

\(f'(x) = 0 \Leftrightarrow x = 1\) hoặc \({\rm{ }}x = 3.\)

Bảng biến thiên của hàm số trên nửa khoảng \([ - 1; + \infty )\):

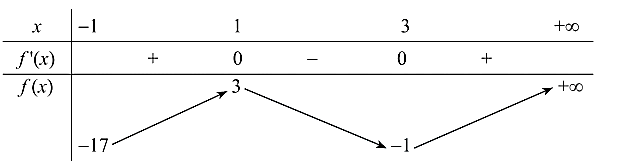
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{_{[ - 1; + \infty )}} f(x) = f( - 1) = - 17\) và hàm số không có giá trị lớn nhất trên \([ - 1; + \infty ).\)

Tập xác định: \(D = \left[ { - 2;2} \right]\).

Ta có: \(y' = \frac{{ - x}}{{\sqrt {4 - {x^2}} }}\) \( \Rightarrow y' = 0 \Leftrightarrow x = 0 \in \left( { - 2;2} \right)\).

Ta có: \(\left\{ \begin{array}{l}y\left( { - 2} \right) = y\left( 2 \right) = 0\\y\left( 0 \right) = 2\end{array} \right. \Rightarrow \mathop {\max }\limits_{\left[ { - 2;\,2} \right]} y = 2\).

a) \(y = \frac{{2x + 1}}{{x - 1}}\)                

1) Tập xác định: \(\mathbb{R}\backslash \{ 1\} \).

2) Sự biến thiên

Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:

\(\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty ,\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty \). Do đó, đường thẳng \(x = 1\) là tiệm cận đứng của đồ thị hàm số\(\mathop {\lim }\limits_{x \to + \infty } y = 2,\mathop {\lim }\limits_{x \to - \infty } y = 2\). Do đó, đường thẳng \(y = 2\) là tiệm cận ngang của đồ thị hàm số.

- \(y' = \frac{{ - 3}}{{{{(x - 1)}^2}}} < 0\) với mọi \(x \ne 1\).

Hàm số nghịch biến trên mỗi khoảng \(( - \infty ;1)\) và \((1; + \infty )\).

Hàm số không có cực trị.

- Bảng biến thiên:

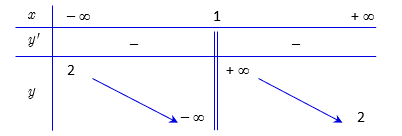
3) Đồ thị

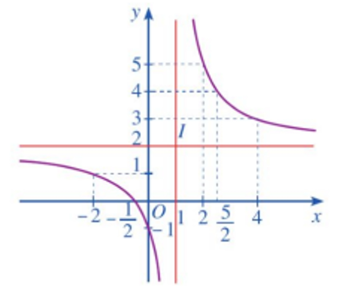
- Giao điểm của đồ thị với trục tung: \((0; - 1)\).

- Giao điểm của đồ thị với trục hoành: \(\left( { - \frac{1}{2};0} \right)\).

Đồ thị hàm số đi qua các điểm \((0; - 1),\left( { - \frac{1}{2};0} \right)\), \(( - 2;1),(2;5),\left( {\frac{5}{2};4} \right)\) và \((4;3)\).

Đồ thị hàm số nhận giao điểm \(I(1;2)\) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

Vậy đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 1}}\) được cho ở Hình.

b) \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\).

1) Tập xác định: \(\mathbb{R}\backslash \{ 1\} \).

2) Sự biến thiên

- Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:

Ta viết hàm số đã cho dưới dạng: \(y = x + \frac{1}{{x - 1}}\).

\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty .\)\(\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty ,\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty \).

Do đó, đường thẳng \(x = 1\) là tiệm cận đứng của đồ thị hàm số.

\(\mathop {\lim }\limits_{x \to + \infty } (y - x) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 1}} = 0,\mathop {\lim }\limits_{x \to - \infty } (y - x) = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 1}} = 0\).

Do đó, đường thẳng \(y = x\) là tiệm cận xiên của đồ thị hàm số

\(y' = \frac{{{x^2} - 2x}}{{{{(x - 1)}^2}}}\)

\(y' = 0 \Leftrightarrow {x^2} - 2x = 0 \Leftrightarrow x = 0\) hoặc \({\rm{ }}x = 2.{\rm{ }}\)

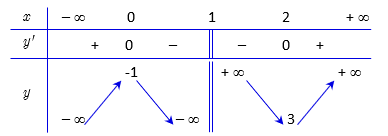
Hàm số đồng biến trên mỗi khoảng \(( - \infty ;0)\) và \((2; + \infty )\); nghịch biến trên mỗi khoảng \((0;1)\) và \((1;2).\)

Hàm số đạt cực đại tại ; đạt cực tiểu tại \(x = 2,{y_{CT}} = 3\).

Bảng biến thiên:

3) Đồ thị

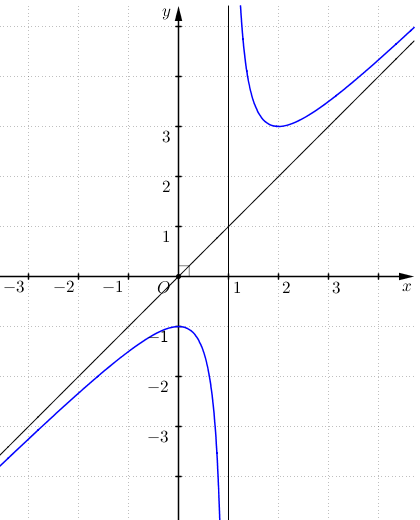
- Giao điểm của đồ thị với trục tung: \((0; - 1)\).

- Đồ thị hàm số không cắt trục hoành.

- Đồ thị hàm số đi qua các điểm \((0; - 1),\left( {\frac{1}{2}; - \frac{3}{2}} \right)\), \(\left( { - 1; - \frac{3}{2}} \right),(2;3),\left( {\frac{3}{2};\frac{7}{2}} \right)\) và \(\left( {3;\frac{7}{2}} \right)\).

- Đồ thị nhận giao điểm \(I(1;1)\) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

Vậy đồ thị hàm số \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\) được cho ở Hình.

a) Ban đầu bình xăng có \(V(0) = 4\) lít xăng.

b) Sau khi bơm 30s, ta có \(V(0,5) = 41,5\)lít.

c) Ta có: \(V'(t) = 300\left( {2t - 3{t^2}} \right)\); Có \(V''\left( t \right) = 300\left( {2 - 6t} \right)\)

\(V'' = 0 \Leftrightarrow t = \frac{1}{3}\).

Có \(V'\left( 0 \right) = 0;V'\left( {\frac{1}{3}} \right) = 100;V'\left( {\frac{1}{2}} \right) = 75\).

Vậy tốc độ tăng thể tích vào thời điểm \(t = \frac{1}{3}\) giây là lớn nhất.

Ta có \(v = s' = - \frac{3}{2}{t^2} + 12t = - \frac{3}{2}\left( {{t^2} - 8t + 16} \right) + 24 = 24 - \frac{3}{2}{\left( {t - 4} \right)^2} \le 24\).

Vậy \(\mathop {\max }\limits_{\left[ {0;\,6} \right]} v\left( t \right) = 24\,\left( {{\rm{m/s}}} \right)\) tại thời điểm \(t = 4\) (giây).