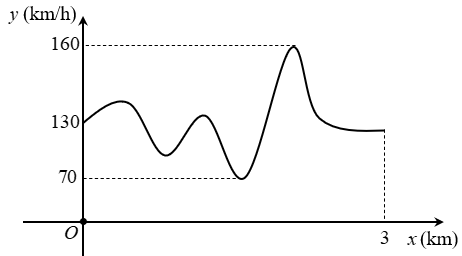
Đề cương ôn tập cuối kì 1 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Bài 2: Tính đơn điệu và cực trị của hàm số
41 người thi tuần này 4.6 1.4 K lượt thi 12 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1
Lời giải
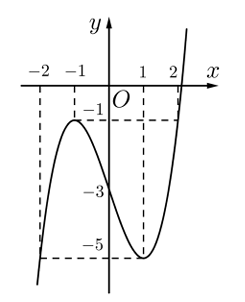
Từ đồ thị ta có: \[\left\{ \begin{array}{l}m = \mathop {\min }\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( { - 2} \right) = - 4\\M = \mathop {\max }\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( { - 1} \right) = 2\end{array} \right. \Rightarrow M + m = - 2\]. Chọn D.
Câu 2
Lời giải
Ta có \(y' = 1 - \frac{4}{{{x^2}}} \Rightarrow y' = 0 \Leftrightarrow {x^2} = 4 \Rightarrow x = 2\) (vì \(x \in \left( {1;5} \right)\)).
Khi đó \(y\left( 1 \right) = 5\), \(y\left( 2 \right) = 4\) và \(y\left( 5 \right) = \frac{{29}}{5}\).
Do đó \(\mathop {\min }\limits_{\left[ {1;5} \right]} y = 4\) tại \(x = 2\). Chọn B.
Câu 3
Lời giải
Ta có \(f'\left( x \right) = 3{x^2} - 16x + 16,f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4 \notin \left( {1;3} \right)\\x = \frac{4}{3} \in \left( {1;3} \right)\end{array} \right.\).
\(f\left( 1 \right) = 0;f\left( {\frac{4}{3}} \right) = \frac{{13}}{{27}};f\left( 3 \right) = - 6\).
Do đó \(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = \frac{{13}}{{27}}\). Chọn B.
Câu 4
Lời giải
Ta có: \(f'\left( x \right) = \left( {2x - 5} \right){e^{2x}}\).
\(f'\left( x \right) = 0 \Leftrightarrow x = \frac{5}{2}\).
Bảng biến thiên của hàm số:
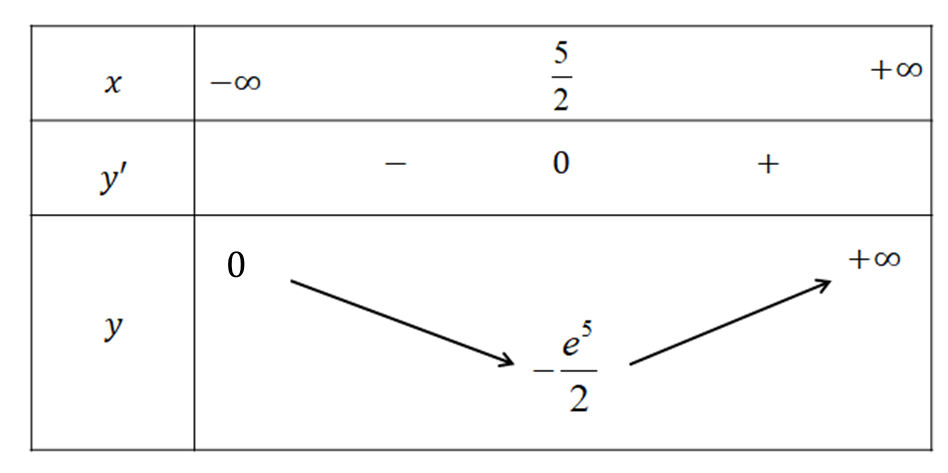
Vậy \(\mathop {\min }\limits_\mathbb{R} f\left( x \right) = - \frac{{{e^5}}}{2}\). Chọn A.
Câu 5
Lời giải
Vì \[s = \frac{1}{3}{t^3} - {t^2} + 9t \Rightarrow v = {t^2} - 2t + 9\].
Xét hàm \[f\left( t \right) = {t^2} - 2t + 9 \Rightarrow f'\left( t \right) = 2t - 2 = 0 \Rightarrow t = 1\].
Bảng biến thiên
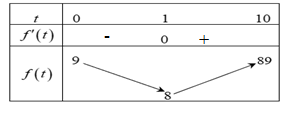
Dựa vào bảng biến thiên ta thấy: \[\mathop {\max }\limits_{\left[ {0;10} \right]} f\left( t \right) = f\left( {10} \right) = 89\].
Vậy vận tốc của vật đạt được lớn nhất bằng \[89\left( {{\rm{m/s}}} \right).\] Chọn A.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Từ đồ thị ta có: \[\left\{ \begin{array}{l}m = \mathop {\min }\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( { - 2} \right) = - 4\\M = \mathop {\max }\limits_{\left[ { - 1 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/10-1761388534.png)